2
Пошаговое объяснение:
1)
Так как НОД(6, 25) = 1, то выполняется теорема Эйлера:
Тогда:
2)
Так как НОД(4, 25) = 1, то выполняется теорема Эйлера:
3)
В итоге:
2
Пошаговое объяснение:
1)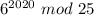
Так как НОД(6, 25) = 1, то выполняется теорема Эйлера:
Тогда:
2)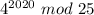
Так как НОД(4, 25) = 1, то выполняется теорема Эйлера:
Тогда:
3)
В итоге: