1. Надо через какую либо вершину провести прямую - например прямая а. 2. от двух других вершин провести перпендикуляры к этой прямой 3. замерить расстояние от этих двух вершин до прямой (то как раз длина этих перпендикуляров.. Например получилось 2 и 3 4. ПО ДРУГУЮ СТОРОНУ от прямой а отложить такие же расстояния (2 и 3) и отметить точки. 5. Соединить эти точки с точкой (вершиной) на прямой а. 6. Полученный треугольник - симметричен первому относительно его вершины (и относительно прямой а тоже, кстати)
Исследуем этот ряд на абсолютную сходимость.
Рассмотрим ряд
Используем предельный признак сравнения:
Значит ряды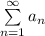 и
и 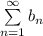
сходятся или расходятся одновременно, но ряд
это гармонический ряд, который расходится. Значит и ряд
расходится.
Исследуем данный в задании ряд на условную сходимость. Используем признак Лейбница. Ряд знакочередующийся.
т.к.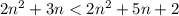 ⇔
⇔ 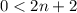 ⇔
⇔ 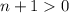 .
.
То есть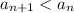 .
.
То есть последовательность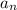 монотонно убвывает.
монотонно убвывает.
То есть последовательность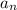 монотонно убвывает и стремится к нулю. Итак, по признаку Лейбница, исходный ряд сходится.
монотонно убвывает и стремится к нулю. Итак, по признаку Лейбница, исходный ряд сходится.
ответ. Сходится условно.
2. от двух других вершин провести перпендикуляры к этой прямой
3. замерить расстояние от этих двух вершин до прямой (то как раз длина этих перпендикуляров.. Например получилось 2 и 3
4. ПО ДРУГУЮ СТОРОНУ от прямой а отложить такие же расстояния (2 и 3) и отметить точки.
5. Соединить эти точки с точкой (вершиной) на прямой а.
6. Полученный треугольник - симметричен первому относительно его вершины (и относительно прямой а тоже, кстати)