Для начала найдём производную данной функции:
Теперь найдём критические точки, приравнивая производную к нулю:
Итак критические точки: .
Устанавливаем знак производной на каждом интервале (см рисунок).
Функция возрастает на каждом из промежутков и .
То есть функция убывает на промежутке .
Для начала найдём производную данной функции:
Теперь найдём критические точки, приравнивая производную к нулю:
Итак критические точки: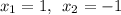 .
.
Устанавливаем знак производной на каждом интервале (см рисунок).
Функция возрастает на каждом из промежутков![(-\infty; \: -1]](/tpl/images/1356/4087/e386e.png) и
и 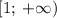 .
.
То есть функция убывает на промежутке![\boxed{[-1; \: 1]}](/tpl/images/1356/4087/52441.png) .
.
ответ: