Возьмем производную данной функции, чтобы затем найти экстремум:
Известно, что производная принимает нулевое значение в точке экстремума ⇒ приравняв производную к нулю мы сможем его найти.
Рассмотрим знак производной до x = 0. При x = -1 производная отрицательна ⇒ функция убывает и при x = 0 минимум (можем так говорить, так как функция обычный куб). Затем производная становиться положительной и функция возрастает, пока x не становиться равен 4. Здесь достигается максимум. Потом производная становиться вновь отрицательной.
ответ: Максимум - (4;29), Минимум - (0;-3)
Пошаговое объяснение:
(Как я понимаю, ночью ставки выше)
Возьмем производную данной функции, чтобы затем найти экстремум:
Известно, что производная принимает нулевое значение в точке экстремума ⇒ приравняв производную к нулю мы сможем его найти.
Рассмотрим знак производной до x = 0. При x = -1 производная отрицательна ⇒ функция убывает и при x = 0 минимум (можем так говорить, так как функция обычный куб). Затем производная становиться положительной и функция возрастает, пока x не становиться равен 4. Здесь достигается максимум. Потом производная становиться вновь отрицательной.
Значит:
При x = 0 -
При x = 4 -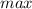
Подставим числа:
ответ: Применяем метод интегрирования по частям и введение под знак дифференциала
Пошаговое объяснение: 1) ∫x·arсtg²xdx= (пусть arсtg²x=U, xdx=dV; тогда 2arctgx dx ·(1/1+x²) = dU, x²/2=dV) =(x²/2)·arсtg²x - (1/2)∫x²2arctgx·dx/(1+x²)= (x²/2)·arсtg²x - ∫x²arctgx dx/ (1+x²) ;
2) Вычислим ∫x²arctgx dx/ (1+x²) =∫(аrctg x - arctg x/(1+x²))dx =∫аrctg x dx - ∫arctg x/(1+x²))dx;
3)∫аrctg x dx=(U=arctg x, dV=dx ⇒dU=1/(1+x²)dx, V=x) =x·arctg x - ∫xdx(1+x²) =x·arctg x - (1/2)·∫d(x²)/(1+x²) =x·arctg x - (1/2)·ln(x²+1) 4) ∫arctg x/(1+x²))dx = ∫d(arctg x)/(1+x²) = (1/2)·arctg²x
Итак: ∫x·arсtg²xdx= (x²/2)·arсtg²x - ∫x²arctgx dx/ (1+x²)=(x²/2)·arсtg²x + (1/2)·ln (x²+1) - x·arctg x + (1/2)·arctg²x +C