По методу рационализации функция с учетом ОДЗ принимает такие же знаки как
(решение методом интервалов прикрепляю)
Найдем сумму длин интервалов.
По методу рационализации функция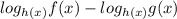 с учетом ОДЗ принимает такие же знаки как
с учетом ОДЗ принимает такие же знаки как 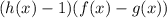
(решение методом интервалов прикрепляю)
Найдем сумму длин интервалов.