Пошаговое объяснение:
Пусть мы верим тому, что уравнение касательной в точке к графику функции - это
(Если надо вывести, напишите в комментариях)
Точка пересечения с осью ОРДИНАТ: (я вас правильно понял?)
В этой точке x = 0
Тогда и
Найдём производную:
Найдём её значение в точке :
Запишем уравнение касательной:
ЕСЛИ ВАМ ЧТО-ТО НЕ ПОНЯТНО, НАПИГИТЕ МНЕ ОБ ЭТОМ В КОММЕНТАРИЯХ
Пошаговое объяснение:
Пусть мы верим тому, что уравнение касательной в точке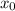 к графику функции
к графику функции 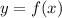 - это
- это 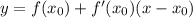
(Если надо вывести, напишите в комментариях)
Точка пересечения с осью ОРДИНАТ: (я вас правильно понял?)
В этой точке x = 0
Тогда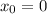 и
и 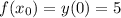
Найдём производную: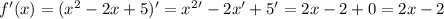
Найдём её значение в точке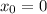 :
:
Запишем уравнение касательной:
ЕСЛИ ВАМ ЧТО-ТО НЕ ПОНЯТНО, НАПИГИТЕ МНЕ ОБ ЭТОМ В КОММЕНТАРИЯХ