Представим себе двудольный граф: слева вершины, обозначающие студентов, справа — вопросы. Если студент ответил на вопрос, то между этим студентом и этим вопросом проведем ребро.
Рассмотрим первую пару вопросов (). Для них по условию найдется хотя бы 6 студентов, каждый из которых ответил правильно ровно на один из этих двух вопросов. Пусть это множество из хотя бы 6 студентов называется . Тогда остальных студентов (тех, что не удовлетворяют описанному требованию) не больше 5 — это множество . Рассмотрим следующую пару вопросов (,попарно отличных от предыдущих). Тогда имеет с хотя бы одно пересечение. Поэтому для пары будет хотя бы одно ребро из множества . Рассматривая далее пары и соответственно пары "берем" еще один элемент из . Так можно продолжать до тех пор, пока все элементы из , коих не больше пяти, не будут взяты. То есть всего можно добавить 2*5=10 вопросов дополнительно к . То есть всего не более 12.
Примечание: множество делится на два множества, из каждого идут ребра к вопросам , но из каждого к ровно одному. Для того, чтобы мы могли всегда изымать элементы из надо всего лишь без ограничения общности потребовать, чтобы ребро из шло в наибольшее из множеств, на которое делится . Тогда наименьшее из этих множеств деления не превосходит 5.
Пусть лягушонок стартует в точке . Тогда, если какие-то две точки повторились, то лягушонок побывал также в точке дважды, т.е. мы попали в цикл. Если мы покажем, что уравнение имеет решение при любом , то цикл будет состоять из всех точек, и лягушонок побывает во всех точках по одному разу, а затем вернется в точку ;
Докажем для начала, что если существует решение для остатков , то существует решение для остатка . Это вполне очевидно: просто сложим два уравнения для остатков . Теперь, в частности, если существует решение для , то существует решение для всех остатков. То есть нам надо решить диофантово уравнение ; Для этого сразу положим ; Пусть ;
Тогда из числа нам нужно получить число ; Но мы умеем прибавлять единицу: . То есть ; Иными словами, получили решение , но нам нужно решение в натуральных числах. Не вопрос: добавим к 2020, а к добавим 99. Получим решение: .
Итак, план действий следующий.
Пусть мы находимся в точке . Прыгаем 41 раз на 100 и 1999 раз на 99. Теперь мы в точке . Таким образом, мы посетим все точки.
Представим себе двудольный граф: слева вершины, обозначающие студентов, справа — вопросы. Если студент ответил на вопрос, то между этим студентом и этим вопросом проведем ребро.
Рассмотрим первую пару вопросов (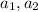 ). Для них по условию найдется хотя бы 6 студентов, каждый из которых ответил правильно ровно на один из этих двух вопросов. Пусть это множество из хотя бы 6 студентов называется
). Для них по условию найдется хотя бы 6 студентов, каждый из которых ответил правильно ровно на один из этих двух вопросов. Пусть это множество из хотя бы 6 студентов называется 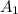 . Тогда остальных студентов (тех, что не удовлетворяют описанному требованию) не больше 5 — это множество
. Тогда остальных студентов (тех, что не удовлетворяют описанному требованию) не больше 5 — это множество 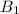 . Рассмотрим следующую пару вопросов (
. Рассмотрим следующую пару вопросов (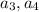 ,попарно отличных от предыдущих). Тогда
,попарно отличных от предыдущих). Тогда 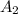 имеет с
имеет с 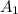 хотя бы одно пересечение. Поэтому для пары
хотя бы одно пересечение. Поэтому для пары 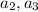 будет хотя бы одно ребро из множества
будет хотя бы одно ребро из множества 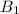 . Рассматривая далее пары
. Рассматривая далее пары 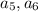 и соответственно пары
и соответственно пары 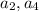 "берем" еще один элемент из
"берем" еще один элемент из 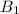 . Так можно продолжать до тех пор, пока все элементы из
. Так можно продолжать до тех пор, пока все элементы из 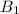 , коих не больше пяти, не будут взяты. То есть всего можно добавить 2*5=10 вопросов дополнительно к
, коих не больше пяти, не будут взяты. То есть всего можно добавить 2*5=10 вопросов дополнительно к 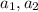 . То есть всего не более 12.
. То есть всего не более 12.
Примечание: множество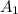 делится на два множества, из каждого идут ребра к вопросам
делится на два множества, из каждого идут ребра к вопросам 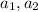 , но из каждого к ровно одному. Для того, чтобы мы могли всегда изымать элементы из
, но из каждого к ровно одному. Для того, чтобы мы могли всегда изымать элементы из 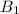 надо всего лишь без ограничения общности потребовать, чтобы ребро из
надо всего лишь без ограничения общности потребовать, чтобы ребро из 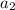 шло в наибольшее из множеств, на которое делится
шло в наибольшее из множеств, на которое делится 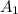 . Тогда наименьшее из этих множеств деления не превосходит 5.
. Тогда наименьшее из этих множеств деления не превосходит 5.
Пусть лягушонок стартует в точке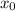 . Тогда, если какие-то две точки повторились, то лягушонок побывал также в точке
. Тогда, если какие-то две точки повторились, то лягушонок побывал также в точке 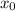 дважды, т.е. мы попали в цикл. Если мы покажем, что уравнение
дважды, т.е. мы попали в цикл. Если мы покажем, что уравнение 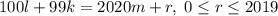 имеет решение при любом
имеет решение при любом  , то цикл будет состоять из всех точек, и лягушонок побывает во всех точках по одному разу, а затем вернется в точку
, то цикл будет состоять из всех точек, и лягушонок побывает во всех точках по одному разу, а затем вернется в точку 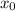 ;
;
Докажем для начала, что если существует решение для остатков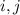 , то существует решение для остатка
, то существует решение для остатка 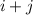 . Это вполне очевидно: просто сложим два уравнения для остатков
. Это вполне очевидно: просто сложим два уравнения для остатков 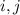 . Теперь, в частности, если существует решение для
. Теперь, в частности, если существует решение для 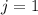 , то существует решение для всех остатков. То есть нам надо решить диофантово уравнение
, то существует решение для всех остатков. То есть нам надо решить диофантово уравнение 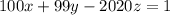 ; Для этого сразу положим
; Для этого сразу положим 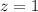 ; Пусть
; Пусть 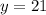 ;
;
Тогда из числа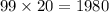 нам нужно получить число
нам нужно получить число 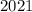 ; Но мы умеем прибавлять единицу:
; Но мы умеем прибавлять единицу: 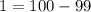 . То есть
. То есть 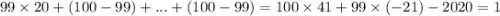 ; Иными словами, получили решение
; Иными словами, получили решение 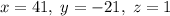 , но нам нужно решение в натуральных числах. Не вопрос: добавим к
, но нам нужно решение в натуральных числах. Не вопрос: добавим к 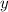 2020, а к
2020, а к  добавим 99. Получим решение:
добавим 99. Получим решение: 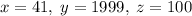 .
.
Итак, план действий следующий.
Пусть мы находимся в точке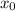 . Прыгаем 41 раз на 100 и 1999 раз на 99. Теперь мы в точке
. Прыгаем 41 раз на 100 и 1999 раз на 99. Теперь мы в точке 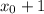 . Таким образом, мы посетим все точки.
. Таким образом, мы посетим все точки.