Решаем данное уравнение как квадратное уравнение относительно
Если D = 0, т.е. a+1 = 0 откуда a = -1, то подставляя этот параметр в исходное уравнение, мы получим
Это уравнение решений не имеет, т.к. левая часть уравнения принимает только положительные значения.
Если , т.е. a + 1 > 0 откуда a>-1, то нам нужны лишь те корни, которые приобретают разные знаки, т.е. по теореме Виета:
Подставим параметры a = 1 и a = 7 в исходное уравнение, получим
a=1 :
Это уравнение корней не имеет, т.к. левая часть уравнения всегда положительно.
a = 7:
Т.е. исходное уравнение имеет единственный корень только при
Решаем данное уравнение как квадратное уравнение относительно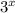
Если D = 0, т.е. a+1 = 0 откуда a = -1, то подставляя этот параметр в исходное уравнение, мы получим
Это уравнение решений не имеет, т.к. левая часть уравнения принимает только положительные значения.
Если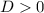 , т.е. a + 1 > 0 откуда a>-1, то нам нужны лишь те корни, которые приобретают разные знаки, т.е. по теореме Виета:
, т.е. a + 1 > 0 откуда a>-1, то нам нужны лишь те корни, которые приобретают разные знаки, т.е. по теореме Виета:
Подставим параметры a = 1 и a = 7 в исходное уравнение, получим
a=1 :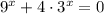
Это уравнение корней не имеет, т.к. левая часть уравнения всегда положительно.
a = 7: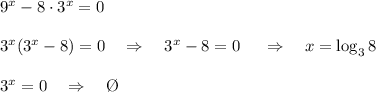
Т.е. исходное уравнение имеет единственный корень только при![a \in (1;7].](/tpl/images/0347/3488/b26cf.png)