Пошаговое объяснение: построим графики выражений в левой и правой частях равенства. Количество точек пересечения графиков совпадает с количеством корней уравнения.
График функции f(x) = |x² - 8x + 12| можно получить, изобразив график функции y = x² - 8x + 12. График функции - парабола с ветвями, направленными вверх. Координаты вершины: , . Рисуем график. Далее отображаем симметрично относительно оси х ту часть графика, которая находится ниже оси х - получаем график функции f(x) = |x² - 8x + 12|.
Графиком функции g(x) = a является горизонтальная прямая, параллельная оси абсцисс. При a = 4 имеем ровно 3 точки пересечения, т.е. ровно 3 корня. Нетрудно заметить, что при других значениях параметра будет или 2, или 4 корня, или же их не будет вообще (при a < 0 графики не будут иметь общих точек).
ответ: a = 4
Пошаговое объяснение: построим графики выражений в левой и правой частях равенства. Количество точек пересечения графиков совпадает с количеством корней уравнения.
График функции f(x) = |x² - 8x + 12| можно получить, изобразив график функции y = x² - 8x + 12. График функции - парабола с ветвями, направленными вверх. Координаты вершины: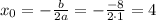
, 
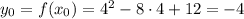. Рисуем график. Далее отображаем симметрично относительно оси х ту часть графика, которая находится ниже оси х - получаем график функции f(x) = |x² - 8x + 12|.
Графиком функции g(x) = a является горизонтальная прямая, параллельная оси абсцисс. При a = 4 имеем ровно 3 точки пересечения, т.е. ровно 3 корня. Нетрудно заметить, что при других значениях параметра будет или 2, или 4 корня, или же их не будет вообще (при a < 0 графики не будут иметь общих точек).