a принадлежит второй четверти, в которой косинус отрицателен,
тогда
но т.к. , то
итак
теперь найдем и .
⇔
а это значит принадлежит первой четверти в которой и синус и косинус положительны, поэтому
a принадлежит второй четверти, в которой косинус отрицателен,
тогда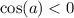
но т.к.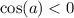 , то
, то
итак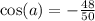
теперь найдем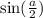 и
и 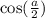 .
.
а это значит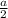 принадлежит первой четверти в которой и синус и косинус положительны, поэтому
принадлежит первой четверти в которой и синус и косинус положительны, поэтому