Из таблицы интегралов:
Применим эту формулу
Это табличный интеграл ∫dx/(x²-a²)=(1/(2a))*㏑I(x-a)/(x+a)I+c
∫dx/(x²-(1/2))=∫dx/(x²-(√2/2)²)=(1/(2*(√2/2)))*㏑I(xx-√2)/(x+√2)I+c=
(√2/2)*㏑I(2x-√2)/(2x+√2)I+c=(√2/2)*㏑I(√2(x√2-1))/(√2(x√2+1)I+c=
(√2/2)*㏑I((x√2-1))/((x√2+1)I+c
Из таблицы интегралов: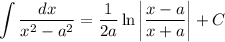
Применим эту формулу
Это табличный интеграл ∫dx/(x²-a²)=(1/(2a))*㏑I(x-a)/(x+a)I+c
∫dx/(x²-(1/2))=∫dx/(x²-(√2/2)²)=(1/(2*(√2/2)))*㏑I(xx-√2)/(x+√2)I+c=
(√2/2)*㏑I(2x-√2)/(2x+√2)I+c=(√2/2)*㏑I(√2(x√2-1))/(√2(x√2+1)I+c=
(√2/2)*㏑I((x√2-1))/((x√2+1)I+c