д)
Пошаговое объяснение:
Известно, что гипотенуза АС прямоугольного треугольника АВС равна 10 и ∠ВАС=60°.
Определим длины катетов АВ и ВС:
AB=AC·cosn60°=10·1/2=5,
BC=AC·sins60°=10·√3/2=5√3.
Собака с поводком длиной 2 двигаясь по катетам АВ и ВС прямоугольного треугольника АВС может достичь (см. рисунок) все точки от А по N и от L по C.
Поэтому, чтобы определить длина части отрезка АС, то есть длину отрезка NL, до которой собака не может добраться определим длину отрезка АN и LC.
Так как ∠MAN=∠BAC, ∠AMN=∠ABC=90°, ∠ANM=∠ACB, то
треугольники ΔAMN и ΔABC подобны. Тогда из-за подобия треугольников ΔAMN и ΔABC:
или AN=AC·MN/BC=10·2/(5√3)=4/√3=4√3/3.
Также ∠LCK=∠ACB, ∠LKC=∠ABC=90°, ∠CLK=∠CAB, то
треугольники ΔLKC и ΔABC подобны. Тогда из-за подобия треугольников ΔLKC и ΔABC:
или LC=AC·LK/AB=10·2/5=4.
Тогда длина части отрезка АС, до которой собака не может добраться
NL=AC-АN-LC=10-4√3/3-4=6-4√3/3.
д)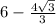
Пошаговое объяснение:
Известно, что гипотенуза АС прямоугольного треугольника АВС равна 10 и ∠ВАС=60°.
Определим длины катетов АВ и ВС:
AB=AC·cosn60°=10·1/2=5,
BC=AC·sins60°=10·√3/2=5√3.
Собака с поводком длиной 2 двигаясь по катетам АВ и ВС прямоугольного треугольника АВС может достичь (см. рисунок) все точки от А по N и от L по C.
Поэтому, чтобы определить длина части отрезка АС, то есть длину отрезка NL, до которой собака не может добраться определим длину отрезка АN и LC.
Так как ∠MAN=∠BAC, ∠AMN=∠ABC=90°, ∠ANM=∠ACB, то
треугольники ΔAMN и ΔABC подобны. Тогда из-за подобия треугольников ΔAMN и ΔABC:
Также ∠LCK=∠ACB, ∠LKC=∠ABC=90°, ∠CLK=∠CAB, то
треугольники ΔLKC и ΔABC подобны. Тогда из-за подобия треугольников ΔLKC и ΔABC:
Тогда длина части отрезка АС, до которой собака не может добраться
NL=AC-АN-LC=10-4√3/3-4=6-4√3/3.
д)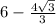
Пошаговое объяснение:
Известно, что гипотенуза АС прямоугольного треугольника АВС равна 10 и ∠ВАС=60°.
Определим длины катетов АВ и ВС:
AB=AC·cosn60°=10·1/2=5,
BC=AC·sins60°=10·√3/2=5√3.
Собака с поводком длиной 2 двигаясь по катетам АВ и ВС прямоугольного треугольника АВС может достичь (см. рисунок) все точки от А по N и от L по C.
Поэтому, чтобы определить длина части отрезка АС, то есть длину отрезка NL, до которой собака не может добраться определим длину отрезка АN и LC.
Так как ∠MAN=∠BAC, ∠AMN=∠ABC=90°, ∠ANM=∠ACB, то
треугольники ΔAMN и ΔABC подобны. Тогда из-за подобия треугольников ΔAMN и ΔABC:
Также ∠LCK=∠ACB, ∠LKC=∠ABC=90°, ∠CLK=∠CAB, то
треугольники ΔLKC и ΔABC подобны. Тогда из-за подобия треугольников ΔLKC и ΔABC:
Тогда длина части отрезка АС, до которой собака не может добраться
NL=AC-АN-LC=10-4√3/3-4=6-4√3/3.