Пусть в данной функции x будет аргументом, а y — параметром:
Это парабола, ветви направлены вниз. Её вершина . Так как , . То есть при функция возрастает при любом допустимом y.
Тогда максимальное значение достигается при x = 4. Подставим это значение в исходную функцию:
Это парабола, ветви направлены вниз. Её максимальное значение достигается в её вершине: . Тогда максимальное значение всей функции при заданных ограничениях достигается в точке (4; 3,5) и равно 48,25.
Минимальное значение достигается при x = 0. Аналогично получаем .
Это парабола, ветви направлены вниз. Так как её вершина , при заданных y функция возрастает. Её наименьшее значение достигается при y = 0. Значит, наименьшее значение всей функции при заданных ограничениях достигается в точке (0; 0) и равно нулю.
Пусть в данной функции x будет аргументом, а y — параметром:
Это парабола, ветви направлены вниз. Её вершина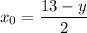
. Так как 
, 
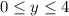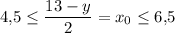. То есть при 
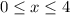функция возрастает при любом допустимом y.
Тогда максимальное значение достигается при x = 4. Подставим это значение в исходную функцию:
Это парабола, ветви направлены вниз. Её максимальное значение достигается в её вершине: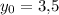
. Тогда максимальное значение всей функции при заданных ограничениях достигается в точке (4; 3,5) и равно 48,25.
Минимальное значение достигается при x = 0. Аналогично получаем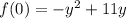
.
Это парабола, ветви направлены вниз. Так как её вершина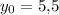
, при заданных y функция возрастает. Её наименьшее значение достигается при y = 0. Значит, наименьшее значение всей функции при заданных ограничениях достигается в точке (0; 0) и равно нулю.
ответ: наибольшее — 48,25; наименьшее — 0.