С вашего разрешения мы и наши партнеры можем использовать точные данные геолокации и проводить идентификацию путем сканирования устройства. Вы можете нажать на кнопку согласия, чтобы согласиться на обработку информации нашей компанией и нашими партнерами, как описано выше. Также вы можете получить доступ к более подробной информации и изменить свои пользовательские настройки, прежде чем дать согласие на обработку информации или отказаться от нее. Обратите внимание, что при обработке ваших персональных данных в некоторых случаях ваше согласие может не потребоваться, однако вы имеете право возразить против такой обработки. Ваши настройки будут применяться только к данному веб-сайту. Вы в любое время можете изменить свои настройки, повторно зайдя на этот сайт, или обратиться к нашей политике
Построим все эти графики в одной системе координат (см. вложение №1). Получившаяся фигура не является криволинейной трапецией, но, проведя прямую (см. вложение №2), можно разбить её на две криволинейные трапеции, у каждой из которых можно найти площадь. Искомая площадь является суммой площадей двух составляющих эту фигуру криволинейных трапеций.
Итак, находим площадь левой криволинейной трапеции.
Теперь находим площадь правой криволинейной трапеции.
С вашего разрешения мы и наши партнеры можем использовать точные данные геолокации и проводить идентификацию путем сканирования устройства. Вы можете нажать на кнопку согласия, чтобы согласиться на обработку информации нашей компанией и нашими партнерами, как описано выше. Также вы можете получить доступ к более подробной информации и изменить свои пользовательские настройки, прежде чем дать согласие на обработку информации или отказаться от нее. Обратите внимание, что при обработке ваших персональных данных в некоторых случаях ваше согласие может не потребоваться, однако вы имеете право возразить против такой обработки. Ваши настройки будут применяться только к данному веб-сайту. Вы в любое время можете изменить свои настройки, повторно зайдя на этот сайт, или обратиться к нашей политике
Построим все эти графики в одной системе координат (см. вложение №1). Получившаяся фигура не является криволинейной трапецией, но, проведя прямую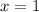 (см. вложение №2), можно разбить её на две криволинейные трапеции, у каждой из которых можно найти площадь. Искомая площадь является суммой площадей двух составляющих эту фигуру криволинейных трапеций.
(см. вложение №2), можно разбить её на две криволинейные трапеции, у каждой из которых можно найти площадь. Искомая площадь является суммой площадей двух составляющих эту фигуру криволинейных трапеций.
Итак, находим площадь левой криволинейной трапеции.
Теперь находим площадь правой криволинейной трапеции.
А теперь складываем и находим искомую площадь.
ответ: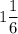 .
.