Найти общее решение дифференциального уравнения первого порядка
x*y' + y - x - 1 = 0
Представим данное дифференциальное уравнение в виде
В левой части уравнения это производная произведения двух функций, т.е.
Проинтегрируем обе части уравнения, получим
Получили общее решение диф. уравнения.
Найти общее решение дифференциального уравнения первого порядка
x*y' + y - x - 1 = 0
Представим данное дифференциальное уравнение в виде
В левой части уравнения это производная произведения двух функций, т.е.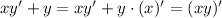
Проинтегрируем обе части уравнения, получим
Получили общее решение диф. уравнения.