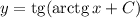Войти Регистрация Спроси ai-bota

Найти общее решение дифференциального уравнения с разделяющимися переменными: y'(1+x^2)=1+y^2

Показать ответ

Ответ:

ludvig9

15.10.2020 15:05

$y'(1 + x^{2}) = 1 + y^{2}$

$\dfrac{dy}{dx} (1 + x^{2}) = 1 + y^{2}$

$\dfrac{dy}{1 + y^{2}}=\dfrac{dx}{1 + x^{2}}$

$\displaystyle \int \dfrac{dy}{1 + y^{2}}=\int \dfrac{dx}{1 + x^{2}}$

$\text{arctg} \, y = \text{arctg} \, x + C$

$y = \text{tg} (\text{arctg} \, x + C)$

ответ: $y = \text{tg} (\text{arctg} \, x + C)$

0,0(0 оценок)

Популярные вопросы: Математика

gusew7kaja

24.07.2020 20:53

Василиса-прекрасная и василиса премудрая разрезали 78метров шёлковой ленты на двенадцатиметровые и пятнадцатиметровые части так что кусков другой длины не осталось.сколько...

nam0

24.07.2020 20:53

26 л сока разлили в 2литровые и 3литровые банки. всего 11 банок. во сколько 2литровых банок разлили сок? заранее буду ....

lsrk

24.07.2020 20:53

На склад поступили детали с трёх станков. на первом станке изготовлено 40% деталей от их общего количества, на втором-35% и на третьем 25%, причем на первом станке было изготовлено...

ленура21

24.07.2020 20:53

Воздушный змей имеет квадратную форму. половина воздушного змея выкрашена красной краской. площадь закрашенной части 2450см2. какой длины планка понадобится, чтобы приклеить...

madhinamelinova

24.07.2020 20:53

Как перевести обыкновенную дробь в десятичную? к примеру как 5/7 или 3/8...

PandaNyya

24.07.2020 20:53

Решите уравнения относительно x: dx * ( a + b)=c (a - b) * ( x + d)=c (a + b) : (x + d)=c dx : (a - b)=c : )...

ЕлизаветаМахова

24.07.2020 20:53

Вмагазине осталось 6 кг яблок,что на 24 кг меньше чем продали.сколько яблок в магазин?...

telytnikovalenp0apjm

24.07.2020 20:53

Ви грали у футбол ваш однокласник упав схопився за ногу йому боляче як йому сплануйте свої дії...

Arina17122002

24.07.2020 20:53

Объем куба 125 см в кубе найти сумму длины всех ребер и сумму площади всех граней...

гуманитарий0013

24.07.2020 20:53

Пеликан выловил за год 1672 рыбы.каждую четвёртую рыбу он съел сам,а остальное скормил своим детям.сколько рыб скормил за год детям папа пеликан?...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку