ответ: y = -x/(x+1) + C(x+1)
Пошаговое объяснение:
Домножим левую и правую части уравнения на , имеем:
ответ: y = -x/(x+1) + C(x+1)
Пошаговое объяснение:
Домножим левую и правую части уравнения на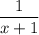 , имеем:
, имеем: