Перепишем уравнение в виде (1+eˣ)*dy/dx=y*eˣ. Это уравнение с разделяющимися переменными, которое приводится к виду dy/y=eˣ*dx/(1+eˣ), или dy/y-d(1+eˣ)/(1+eˣ). Интегрируя обе части, получаем ln(y)-ln(1+eˣ)=ln(C), или y/(1+eˣ)=C.
Проверка:
y=C*(1+eˣ), y'=C*eˣ, (1+eˣ)*C*eˣ=C*(1+eˣ)*eˣ. Так как получено тождество, то решение найдено верно.
ответ: y/(1+eˣ)=C.
Пошаговое объяснение:
Перепишем уравнение в виде (1+eˣ)*dy/dx=y*eˣ. Это уравнение с разделяющимися переменными, которое приводится к виду dy/y=eˣ*dx/(1+eˣ), или dy/y-d(1+eˣ)/(1+eˣ). Интегрируя обе части, получаем ln(y)-ln(1+eˣ)=ln(C), или y/(1+eˣ)=C.
Проверка:
y=C*(1+eˣ), y'=C*eˣ, (1+eˣ)*C*eˣ=C*(1+eˣ)*eˣ. Так как получено тождество, то решение найдено верно.
ответ: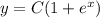 .
.
Пошаговое объяснение: