Пошаговое объяснение:
===========
Есть готовый интеграл
Сразу скажу: как это доказать, я не знаю.
У нас а = 1, получается:
Подставляем пределы интегрирования
Пошаговое объяснение:
===========
Пошаговое объяснение:
Есть готовый интеграл
Сразу скажу: как это доказать, я не знаю.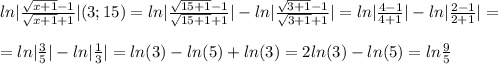
У нас а = 1, получается:
Подставляем пределы интегрирования