Воспользуемся интегралами для решения данной задачи. Если просто решить уравнения, то получим, что ограниченная область лежит на отрезке x ∈ [0,2]. У параболы и у прямой никаких выколотых точек и других проблем там нет => можем брать определенный интеграл. Определять площадь фигуры будем определять через разность двух определенных интегралов:
Площадь под параболой определим через этот интеграл( пусть будет S1):
S1 =
Теперь посчитаем площадь под прямой и назовем ее S2(можно делать и трапецией)
S2 = 8;
Теперь вычтем из S2, S1 и получим площадь фигуры S:
S = S2 -S1 =
(Если нужно, первообразная параболы будет x^3/3 + 2x, а первообразная прямой x^2 + 2x)
ответ: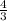
Пошаговое объяснение:
Воспользуемся интегралами для решения данной задачи. Если просто решить уравнения, то получим, что ограниченная область лежит на отрезке x ∈ [0,2]. У параболы и у прямой никаких выколотых точек и других проблем там нет => можем брать определенный интеграл. Определять площадь фигуры будем определять через разность двух определенных интегралов:
Площадь под параболой определим через этот интеграл( пусть будет S1):
S1 =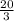
Теперь посчитаем площадь под прямой и назовем ее S2(можно делать и трапецией)
S2 = 8;
Теперь вычтем из S2, S1 и получим площадь фигуры S:
S = S2 -S1 =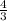
(Если нужно, первообразная параболы будет x^3/3 + 2x, а первообразная прямой x^2 + 2x)
===================================
Пошаговое объяснение: