Построим график функции y=6+5x-x^2. Получилась парабола, которая пересекается с прямой y = 0( ось OX) в точках -1 и 6 по иксу. Значит будем искать площадь фигуры на промежутке [-1;6] - пределы интегрирования.
S = ед^2
Построим график функции y=6+5x-x^2. Получилась парабола, которая пересекается с прямой y = 0( ось OX) в точках -1 и 6 по иксу. Значит будем искать площадь фигуры на промежутке [-1;6] - пределы интегрирования.
S =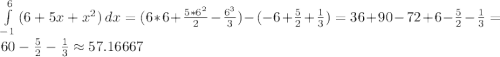 ед^2
ед^2