Пошаговое объяснение:
Площадь фигуры, ограниченной данными линиями, можно получить, отняв от площади трапеции с основаниями 1 и 3 и высотой 2 площадь криволинейной трапеции, ограниченной линиями , и .
Площадь трапеции равна
Площадь криволинейной трапеции равна от 1 до 3.
То есть,
Таким образом, искомая площадь фигуры равна
.
Пошаговое объяснение:
Площадь фигуры, ограниченной данными линиями, можно получить, отняв от площади трапеции с основаниями 1 и 3 и высотой 2 площадь криволинейной трапеции, ограниченной линиям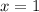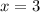и
, 
и 
.
Площадь трапеции равна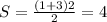
Площадь криволинейной трапеции равна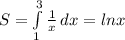
от 1 до 3.
То есть,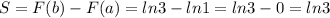
Таким образом, искомая площадь фигуры равна