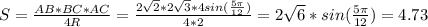Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
serob1223
10.05.2023 05:54 •
Математика
Найти площадь треугольника, вписанного в круг радиуса 2 см, если два угла треугольника равны π/3 и π/4.
Показать ответ
Ответ:
Sabaydin
15.10.2020 15:31
см^2
Пошаговое объяснение:
1) Сначала находим угол А:
2) По теореме синусов:
3)
0,0
(0 оценок)
Популярные вопросы: Математика
kutina1969
13.01.2021 13:37
Решите задачу по экономике...
koschka2000
04.10.2022 01:34
Какой цифрой оканчивается разность чисел В8ЛО-5Ц4?...
атвсомсча
01.12.2020 17:25
1) Для джема на 5 чашек клубники берут з чашки сахару. Сколько надо вз сахару на 25 кг клубники?...
warfrsm
14.01.2023 02:54
7 целых + 2/3 + 4 целых 5/6 + 2 1/4 (...
Kykyshka2000
29.10.2021 12:12
Найдите корни уровнений номер 677,678...
kazekb
18.10.2020 07:43
Решите Кто решит поставлю как лучший ответ...
11264чс
01.08.2022 15:48
617. Выполните действия: 1 1 3 11)12 6 8+15114);3):316684152451-2)) -1)4)9347 391220...
Маринка200711
07.09.2022 16:11
У банку на вклади громадян нараховують 7 % річних. Скільки гривень було покладено на рахунок у банк, якщо через рік на рахунку стало 12 840 грн?...
leron9999
03.04.2023 12:35
Частное от деления двух чисел равно 12,8. как изменится частное, если: а. делимое увеличим в 1,5 раза? б. делитель увеличим в 3,2 раза? в. делимое умножим на 3,5, а делитель...
0оМорковкао0
17.04.2023 01:39
На вывязывание каждого из четырёх шарфиков нужно 75 г козьего пуха. Уже израсходовали 0,4 всей приготовленной для этих шарфиков пряжи. Сколько граммов пуха осталось?Укажите...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Пошаговое объяснение:
1) Сначала находим угол А:
2) По теореме синусов:
3)