В этой задаче есть два хороших к решению. Полностью аналитический и схематично-графический. Я люблю решать графически, но аналитический метод тоже покажу.
1: схематично-графический
Введем функцию . Это парабола, ветви которой направлены вверх. Изобразим возможные расположения графика, которые удовлетворяют условию задачи (я рисовать не буду; если у вас появятся вопросы, пишите; будет время отвечу)
Опишем эти случаи:
/или/
Замечу, что в первом случае писать условие нет необходимости, так как, если какой-то элемент параболы ниже оси OX, то корня заведомо будет два.
Выполним необходимые вычисления:
, где - это координата вершины параболы .
Перепишем случаи, опираясь на записанные выше данные:
/или/
Решая полученное, приходим к ответу:
2: аналитический
Уравнение является квадратным, а значит его можно решить относительно через дискриминант, причем сразу поделим его на 4, чтобы упростить счет (можно не делить, но цифры вначале будут менее приятные):
При (то есть, когда ):
Выразим корни уравнения:
Хорошо видно, что . Тогда, если , то тоже меньше минус единицы, что нас не устраивает. Поэтому здесь возможет единственный случай:
Учитывая все выше сказанное приходим к тому, что .
При (то есть, когда или ):
В этом случае корни совпадают, то есть . Наша задача состоит в том, чтобы подчинить его условию , что возможно, если . Данный случай достижим либо при , либо при . Так как , то подходит только .
Пусть по норме ежедневно вспахивалось х га , тогда 180 га будет вспахано за 180/х дней.
Но фактически ежедневно вспахивалось (х+2) га , тогда 180 га будет вспахано за 180/(х+2). дней.
Все поле фактически было вспахано на 1 день раньше , составим уравнение 180/х -180/(х+2)=1.
Умножим обе части на х(х+2)≠0 те х≠0, х≠-2
180(х+2)-180х=х(х+2)
х²+2х-360 =0
По т.Виета х₁+х₂=-2 , х₁*х₂=-360 ⇒ х₁= 18 , х₂=-20 не подходит по смыслу задачи.
Фактически вспахал за 180:(18+2)=9
ответ. тракторист вспахал поле за 9 дней
(см. объяснение)
Пошаговое объяснение:
В этой задаче есть два хороших к решению. Полностью аналитический и схематично-графический. Я люблю решать графически, но аналитический метод тоже покажу.
1: схематично-графический
Введем функцию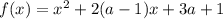 . Это парабола, ветви которой направлены вверх. Изобразим возможные расположения графика, которые удовлетворяют условию задачи (я рисовать не буду; если у вас появятся вопросы, пишите; будет время отвечу)
. Это парабола, ветви которой направлены вверх. Изобразим возможные расположения графика, которые удовлетворяют условию задачи (я рисовать не буду; если у вас появятся вопросы, пишите; будет время отвечу)
Опишем эти случаи:
Замечу, что в первом случае писать условие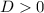 нет необходимости, так как, если какой-то элемент параболы ниже оси OX, то корня заведомо будет два.
нет необходимости, так как, если какой-то элемент параболы ниже оси OX, то корня заведомо будет два.
Выполним необходимые вычисления:
Перепишем случаи, опираясь на записанные выше данные:
Решая полученное, приходим к ответу:
2: аналитический
Уравнение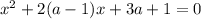 является квадратным, а значит его можно решить относительно
является квадратным, а значит его можно решить относительно  через дискриминант, причем сразу поделим его на 4, чтобы упростить счет (можно не делить, но цифры вначале будут менее приятные):
через дискриминант, причем сразу поделим его на 4, чтобы упростить счет (можно не делить, но цифры вначале будут менее приятные):
При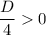 (то есть, когда
(то есть, когда 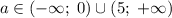 ):
):
Выразим корни уравнения:
Хорошо видно, что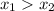 . Тогда, если
. Тогда, если 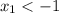 , то
, то  тоже меньше минус единицы, что нас не устраивает. Поэтому здесь возможет единственный случай:
тоже меньше минус единицы, что нас не устраивает. Поэтому здесь возможет единственный случай:
Учитывая все выше сказанное приходим к тому, что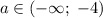 .
.
При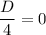 (то есть, когда
(то есть, когда 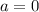 или
или 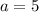 ):
):
В этом случае корни совпадают, то есть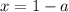 . Наша задача состоит в том, чтобы подчинить его условию
. Наша задача состоит в том, чтобы подчинить его условию 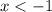 , что возможно, если
, что возможно, если 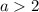 . Данный случай достижим либо при
. Данный случай достижим либо при 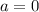 , либо при
, либо при 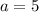 . Так как
. Так как 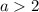 , то подходит только
, то подходит только 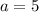 .
.
Объединим найденное:
Задание выполнено!