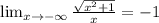Сначала учтем, что поскольку у нас стремление к то х будет отрицательным. Дальше преобразуем выражение:
Теперь находим предел:
Почему -1, потому что по сути в числителе у нас явно положительное число, и после наших преобразований оно и должно им остаться. а вот знаменатель при стремлении к будет отрицательным. Если делить положительное на отрицательное, то в результате получается отрицательное.
Сначала учтем, что поскольку у нас стремление к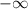 то х будет отрицательным. Дальше преобразуем выражение:
то х будет отрицательным. Дальше преобразуем выражение:
Теперь находим предел:
Почему -1, потому что по сути в числителе у нас явно положительное число, и после наших преобразований оно и должно им остаться. а вот знаменатель при стремлении к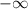 будет отрицательным. Если делить положительное на отрицательное, то в результате получается отрицательное.
будет отрицательным. Если делить положительное на отрицательное, то в результате получается отрицательное.
ответ: