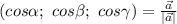У нас дана функция 3-х переменных, значит, говоря про производную по направлению, ее направляющий вектор должен иметь 3 координаты. А в трехмерном пространстве система координат делится на октанты, а не квадранты!
Биссектриса 1-го октанта имеет направляющий вектор: a⁻=(1,1,1)
√3
Пошаговое объяснение:
У нас дана функция 3-х переменных, значит, говоря про производную по направлению, ее направляющий вектор должен иметь 3 координаты. А в трехмерном пространстве система координат делится на октанты, а не квадранты!
Биссектриса 1-го октанта имеет направляющий вектор: a⁻=(1,1,1)
А дальше пользуемся формулой:
где