формула для производной сложной функции нескольких переменных
функция задана в виде , тогда производная имеет вид
для нашего случая посчитаем
и тогда ответ
(здесь мы не будем заменять х на 4t-5, и у на t³, хотя и можно было. но, как правило, когда функция изначально предложена в "замысловатом" виде, то будет логичным оставить в таком же виде и результаты)
Пошаговое объяснение:
формула для производной сложной функции нескольких переменных
функция задана в виде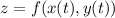 , тогда производная имеет вид
, тогда производная имеет вид
для нашего случая посчитаем
и тогда ответ
(здесь мы не будем заменять х на 4t-5, и у на t³, хотя и можно было. но, как правило, когда функция изначально предложена в "замысловатом" виде, то будет логичным оставить в таком же виде и результаты)