Ряд сходится при и при расходится по признаку Коши.
Тогда радиус сходимости равен 1, а интервал получим из неравенства
ответ: 1; (-2;0)
____________________________
Степенной ряд имеет вид
Тогда последовательность коэффициентов степенного ряда разбивается на 2 подпоследовательности:
Тогда используем формулу Коши-Адамара:
Ряд сходится при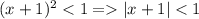 и при
и при 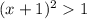 расходится по признаку Коши.
расходится по признаку Коши.
Тогда радиус сходимости равен 1, а интервал получим из неравенства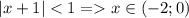
ответ: 1; (-2;0)
____________________________
Степенной ряд имеет вид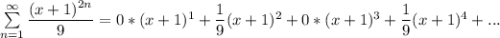
Тогда последовательность коэффициентов степенного ряда разбивается на 2 подпоследовательности: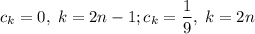
Тогда используем формулу Коши-Адамара: