Пусть x см длина прямоугольного параллелепипеда. Тогда (3x) см его ширина , а высота (x+14) см . Сумма длин всех ребер прямоугольного параллелепипеда определяется по формуле : L =4*(a+b+c) , где а- длина , b-ширина , а с - высота прямоугольного параллелепипеда . 4∗(3x+x+x+14)=376;5x+14=376:4;5x+14=94;5x=94−14;5x=80;x=80:5;x=16.
Значит 16 см - ширина прямоугольного параллелепипеда.
16*3=48 см - длина .
16+14=30 см - высота.
Среднее арифметическое чисел - это сумма всех чисел, делённая на их количество.
Выражение: (8 × 4 - 6) : 5 = 5,2.
1) 8 × 4 = 32 - на столько увеличится сумма четырёх чисел;
2) 32 - 6 = 26 - на столько увеличится сумма пяти чисел;
3) 26 : 5 = 5,2 - на столько увеличится среднее арифметическое пяти чисел.
Пошаговое объяснение:
48 см, 16 см, 30 см.
Пошаговое объяснение:
Пусть x см длина прямоугольного параллелепипеда. Тогда (3x) см его ширина , а высота (x+14) см . Сумма длин всех ребер прямоугольного параллелепипеда определяется по формуле : L =4*(a+b+c) , где а- длина , b-ширина , а с - высота прямоугольного параллелепипеда . 4∗(3x+x+x+14)=376;5x+14=376:4;5x+14=94;5x=94−14;5x=80;x=80:5;x=16.
Значит 16 см - ширина прямоугольного параллелепипеда.
16*3=48 см - длина .
16+14=30 см - высота.
Среднее арифметическое чисел - это сумма всех чисел, делённая на их количество.
Выражение: (8 × 4 - 6) : 5 = 5,2.
1) 8 × 4 = 32 - на столько увеличится сумма четырёх чисел;
2) 32 - 6 = 26 - на столько увеличится сумма пяти чисел;
3) 26 : 5 = 5,2 - на столько увеличится среднее арифметическое пяти чисел.
ответ: увеличится на 5,2.
среднее арифметическое увеличится на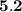
.
Решение:Пусть имеющиеся у нас пять чисел - это
, 
, 
, 
, 
.
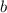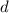Их среднее арифметическое равно:
Пока ничего сложного. Но дальше - хуже, так как одно число уменьшилось на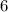
, а остальные четыре - увеличились на 
!
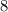Но все же не так плохо: с учетом этих данных мы можем составить буквенное выражение для среднего арифметического и даже упростить его:
Получаем, что среднее арифметическое "теперь" - это среднее арифметическое "тогда", и еще прибавить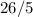
.
Делаем, вывод, что среднее арифметическое изменилось (увеличилось) на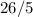
или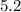 
.
Задача решена!