(см. объяснение)
Пошаговое объяснение:
По определению:
Из основного тригонометрического тождества с учетом того, что , следует:
Тогда:
Подставим значение синуса из условия в формулу:
Задание выполнено!
Замечу, что можно было воспользоваться готовой формулой:
Откуда бы получили:
И, очевидно, что положительный корень посторонний.
(см. объяснение)
Пошаговое объяснение:
По определению:
Из основного тригонометрического тождества с учетом того, что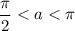 , следует:
, следует:
Тогда:
Подставим значение синуса из условия в формулу:
Задание выполнено!
Замечу, что можно было воспользоваться готовой формулой:
Откуда бы получили:
И, очевидно, что положительный корень посторонний.