При , очевидно, уравнение имеет ровно одно решение - , попадающее в заданный интервал. Соответственно, данное значение параметра пойдет в ответ.
Далее рассмотрим два случая:
Предположим, корни уравнения - отрицательные, т.е. . Уравнение принимает вид:
.
Проверяем найденный корень на попадение в интервал :
Предположим, корни уравнения - положительные, т.е. . Уравнение принимает вид .
Проверяем найденный корень на попадение в интервал - очевидно, .
Анализируем. Заметим, что значения подпадают под оба случая: при таких значениях параметра на интервале существует как первый корень , так и второй - . Т.к. корень должен быть всего один, все необходимо исключить из ответа.
Для на отрезке существует только один корень - , поэтому данные значения параметра идут в ответ.
Далее рассмотрим два случая:
Предположим, корни уравнения - отрицательные, т.е.Проверяем найденный корень на попадение в интервал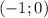 :
:
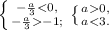
Предположим, корни уравнения - положительные, т.е.Проверяем найденный корень на попадение в интервал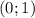 - очевидно,
- очевидно, 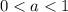 .
.
Анализируем. Заметим, что значения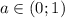 подпадают под оба случая: при таких значениях параметра на интервале существует как первый корень
подпадают под оба случая: при таких значениях параметра на интервале существует как первый корень 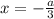 , так и второй -
, так и второй -  . Т.к. корень должен быть всего один, все
. Т.к. корень должен быть всего один, все 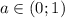 необходимо исключить из ответа.
необходимо исключить из ответа.
Для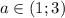 на отрезке существует только один корень -
на отрезке существует только один корень - 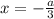 , поэтому данные значения параметра идут в ответ.
, поэтому данные значения параметра идут в ответ.
ОТВЕТ: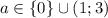 .
.