Найти значение производной в точке x0
f(x) = 3x^2+8x+3 x0=1
f(x)= x-18/x x0=3
f(x)= 2x^2*cosx, x0= п/4
найдите производную функции
f(x) = 2^4x-1
f(x) = ln (x^3+5x)

1) 14

2) 2 или 3 (см.решение)

3)

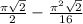
4)

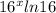
или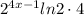 (см.решение)

5)

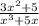
Пошаговое объяснение:

1)

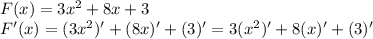
Производная от константы (от тройки), равна нулю.

Производная от равна единице.

Производная от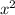 равна .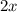

Подставляем :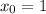

2.1) Если имелось в виду следующее: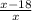

То здесь надо использовать формулу для производной от частного:

Подставляем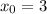

2.2) Если имелось в виду следующее: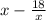

Подставляем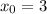

3)

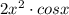
Используем формулу для производной от произведения:

Подставляем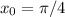

4.1) Если имелось в виду следующее:

4.2) Если имелось в виду следующее:

Используется формула для вычисление производной от сложной функции:

5)

Дифференциируем по правилу для сложной функции: