№1. "Ширина прямоугольника, равная р метров, составляет 1/3 стороны квадрата" - значит, сторона квадрата = 3р. "Ширина прямоугольника составляет 3/4 его длины" - значит, длина прямоугольника = 4/3 ширины или 4/3 р. Площадь квадрата = (3р)²= 9р², площадь прямоугольника = 4/3р*р= 4/3 р².
Сравним: площадь квадрата больше площади прямоугольника в 9:4/3 раза= 9*3/4=27/4 раза. % - сотая часть числа. Площадь квадрата составляет (2700/4=>) 675% площади прямоугольника/
№2 "Длина прямоугольника к метров.Его ширина составляет 3/4 длины" - значит, ширина = 3/4 к. "Сторона квадрата составляет 4/3 длины прямоугольника" - значит, = 4/3 к. Периметр прямоугольника = 2 (к+3/4 к)=7/2 к. Периметра квадрата = 4*4/3 к= 16/3 к.
Сравним: периметр прямоугольника составляет 7/2 к :16/3 к = 21/32 от периметра квадрата. Это 2100/32=65,625%
"Ширина прямоугольника, равная р метров, составляет 1/3 стороны квадрата" - значит, сторона квадрата = 3р.
"Ширина прямоугольника составляет 3/4 его длины" - значит, длина прямоугольника = 4/3 ширины или 4/3 р.
Площадь квадрата = (3р)²= 9р², площадь прямоугольника = 4/3р*р= 4/3 р².
Сравним: площадь квадрата больше площади прямоугольника в 9:4/3 раза= 9*3/4=27/4 раза.
% - сотая часть числа.
Площадь квадрата составляет (2700/4=>) 675% площади прямоугольника/
№2
"Длина прямоугольника к метров.Его ширина составляет 3/4 длины" - значит, ширина = 3/4 к.
"Сторона квадрата составляет 4/3 длины прямоугольника" - значит, = 4/3 к.
Периметр прямоугольника = 2 (к+3/4 к)=7/2 к.
Периметра квадрата = 4*4/3 к= 16/3 к.
Сравним: периметр прямоугольника составляет 7/2 к :16/3 к = 21/32 от периметра квадрата. Это 2100/32=65,625%
ответ: 8 пар.
Объяснение:
Раскрыв скобки, получаем:
Перенесем слагаемые с переменными влево, а свободный член — вправо:
Из обеих частей уравнения вычтем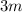 :
:
Разложим левую часть на множители методом группировки:
К обеим частям уравнения прибавим выражение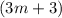 :
:
Вынесем общий множитель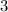 за скобки:
за скобки:
Вынесем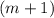 :
:
Так значения m и n целые (по нужному условию), значения выражений в скобках не могут быть дробными.
Произведение двух целых чисел равно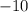 в восьми случаях:
в восьми случаях:
1)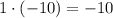 ;
;
2)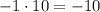 ;
;
3)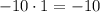 ;
;
4)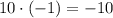 ;
;
5)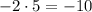 ;
;
6)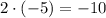 ;
;
7)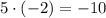 ;
;
8)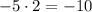 .
.
Определим, какие будут значения m и n, если значения выражений в скобках равны множителям из каждого случая:
1)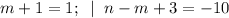
Получаем:
Значит, (m,n) = (0; -13).
Аналогично рассмотрим следующие случаи:
2)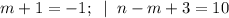
(m,n) = (-2; 5).
3)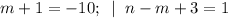
(m,n) = (-11; -13).
4)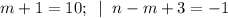
(m,n) = (9; 5).
5)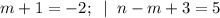
(m,n) = (-3; -1).
6)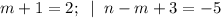
(m,n) = (1; -7).
7)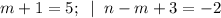
(m,n) = (4; -1).
8)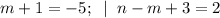
(m,n) = (-6; -7).
Выходит, 8 пар целых чисел (m, n) удовлетворяют данное равенство.