Если число кратно 45, то оно кратно 9 и 5. Если число делится на 9, то его сумма цифр делится на 9. Если число делится на 5, то последняя цифра - 0 или 5. У нас все цифры должны быть четны, значит, последняя цифра 0. Теперь нам нужно найти три первых цифры, которые в сумме делятся на 9. Если сумма трех цифр равна 9, то хотя бы одно из них нечетное. Значит, их сумма равна 18. Это тройки (4, 6, 8), (6, 6, 6), и (2, 8, 8). Можно перечислить ВСЕ такие числа: 4680, 4860, 6480, 6840, 8460, 8640, 6660, 2880, 8280, 8820 Выбирай любое.
Берём, скажем, точку как отправную, и размножаем векторы и , используя параметры и :
Отсюда параметрические уравнения:
Неявное уравнение
В уравнении коэффициенты A, B, C - это координаты вектора нормали, а D - коэффициент, сдвигающий плоскость, задаваемую вектором нормали, так, чтобы плоскость содержала в себе одну из точек из условия.
Найдём вектор нормали как векторное произведение векторов и :
Итого
Предварительный вид неявного уравнения:
Найдём D, подставив какую-нибудь из точек из условия, скажем, С:
Если число делится на 9, то его сумма цифр делится на 9.
Если число делится на 5, то последняя цифра - 0 или 5.
У нас все цифры должны быть четны, значит, последняя цифра 0.
Теперь нам нужно найти три первых цифры, которые в сумме делятся на 9.
Если сумма трех цифр равна 9, то хотя бы одно из них нечетное.
Значит, их сумма равна 18. Это тройки (4, 6, 8), (6, 6, 6), и (2, 8, 8).
Можно перечислить ВСЕ такие числа:
4680, 4860, 6480, 6840, 8460, 8640, 6660, 2880, 8280, 8820
Выбирай любое.
Параметрические уравнения:
Неявное уравнение:
Пошаговое объяснение:
Параметрическое уравнение
Вектор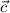 :
:
Вектор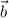 :
:
Берём, скажем, точку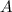 как отправную, и размножаем векторы
как отправную, и размножаем векторы 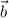 и
и 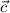 , используя параметры
, используя параметры  и
и 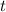 :
:
Отсюда параметрические уравнения:
Неявное уравнение
В уравнении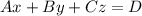 коэффициенты A, B, C - это координаты вектора нормали, а D - коэффициент, сдвигающий плоскость, задаваемую вектором нормали, так, чтобы плоскость содержала в себе одну из точек из условия.
коэффициенты A, B, C - это координаты вектора нормали, а D - коэффициент, сдвигающий плоскость, задаваемую вектором нормали, так, чтобы плоскость содержала в себе одну из точек из условия.
Найдём вектор нормали как векторное произведение векторов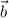 и
и 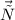 :
:
Итого
Предварительный вид неявного уравнения:
Найдём D, подставив какую-нибудь из точек из условия, скажем, С:
Итого: