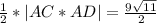Нефтеразведывательная компания получила финансирование для проведения 6 нефтеразработок. Вероятность успешной нефтеразведки 0,05 . Предположим, что нефтеразведку осуществляет независимые друг от друга разведывательные партии. Найдите вероятность того, что две нефтеразведки принесут успех. ​

1500 см^3 - объём коробки

500 см^2 - сумма площадей боковых граней коробки

Пошаговое объяснение:

Коробка имеет форму прямоугольного параллелепипеда, противоположные грани которого равны между собой.  Объём коробки (прямоугольного параллелепипеда), равен произведению площади основания на высоту: V=a*b*h, где a – длина параллелепипеда = 15 см,  b – ширина параллелепипеда = 10 см и h - высота прямоугольного параллелепипеда = 10 см.

V = 15 * 10 * 10 = 1500 см^3 - объём коробки

Коробка, или прямоугольный параллелепипед имеет 4 боковых грани плюс 2 грани нижняя и верхняя.

По условию задания нужно найти  сумму площадей боковых граней коробки.

Сначала вычислим сумму площадей всех граней прямоугольного параллелепипеда, для чего вычислим площадь только 3 граней, суммируем их и умножим на 2:

S1 = a * b = 15* 10 = 150 см^2

S2 = b * h = 10 * 10 = 100 см^2

S3 = a * h = 15 * 10 = 150 см^2

Сумма площадей боковых граней прямоугольного параллелепипеда равна: S бок.гр. = (S2 + S3) * 2 = (100 + 150) * 2 = 500 см^2

Сумма площадей всех граней прямоугольного параллелепипеда равна : S общ. = (S1 +  S2 + S3) * 2 = (150 + 100 + 150) * 2 = 800 см^2.

S=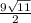; V=3

Пошаговое объяснение:

Даны координаты пирамиды: A1(1,3,1), B(-1,4,6), C(-2,-3,4), D(3,4,-4)

Объем пирамиды, построенной на векторах AB(X1;Y1;Z1), AC(X2;Y2;Z2), AD(X3;Y3;Z3) равен:

здесь X,Y,Z координаты вектора.

Найдем вектора:

AB(-2;1;5)

AC(-3;-6;3)

AD(2;1;-5)

 = = 3

Где (-18) нашли как определитель матрицы.

∆ = -2*((-6)*(-5) - 1*3) - -3*(1*(-5) - 1*5) + 2*(1*3 - (-6)*5) = -18

Площадь грани ACD находим как половину модуля векторного произведения векторов AC и AD

AC(-3;-6;3)

AD(2;1;-5)

S=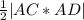

векторное произведение

AC*AD = = i ((-6)·(-5) - 3·1) - j ((-3)·(-5) - 3·2) + k ((-3)·1 - (-6)·2) = i (30 - 3) - j (15 - 6) + k (-3 + 12) = {27; -9; 9}

Модуль вектора

|AC*AD| =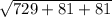 = √891 = 9√11

S=