Некоторое четырехзначное число является точным квадратом. если убрать первую цифру слева, то оно станет точным кубом, а если убрать 2 первые цифры, то оно станет четвертой степенью целого числа. найдите это число.
Если убрать две первые цифры, то получится двузначное число, которое, согласно условию, является четвертой степенью целого числа. Среди двузначных чисел таких всего два: 16=2⁴ и 81=3⁴;
Если убрать первую цифру слева, то получим трехзначное число - куб по условию. Кубов среди трехзначных чисел немного, вот они: 5³, 6³, 7³, 8³ и 9³. При этом последние две цифры должны быть 16 или 81 (см. выше).
Таким образом, подходит только 6³. Остается найти число x такое, что x216 - квадрат. Можно записать: ; Взяв это равенство по модулю 3, получим: (так как квадрат числа дает остаток или 1, или 0 при делении на 3).
Значит, x равен 1, 3, 4, 6, 7 или 9. (можно было объяснить проще: x+2+1+6 - сумма цифр искомого числа дает тот же остаток от деления на 3, что и само число [известное свойство], откуда и вытекает полученное). Можно перебрать оставшиеся числа, а можно предположить, что число делится на три. Тогда остаются числа 3, 6, 9. Более того, искомое число делится и на 4. Значит, число делится на 12. Осталось проверить квадраты чисел 36, 48, 60, 72, 84, 96. Но искомое число оканчивается на 6, поэтому к рассмотрению подлежат лишь 36 и 96. Легкой проверкой убеждаемся, что 96 подходит. Искомое число - 9216
Если убрать две первые цифры, то получится двузначное число, которое, согласно условию, является четвертой степенью целого числа. Среди двузначных чисел таких всего два: 16=2⁴ и 81=3⁴;
Если убрать первую цифру слева, то получим трехзначное число - куб по условию. Кубов среди трехзначных чисел немного, вот они: 5³, 6³, 7³, 8³ и 9³. При этом последние две цифры должны быть 16 или 81 (см. выше).
Таким образом, подходит только 6³. Остается найти число x такое, что x216 - квадрат. Можно записать: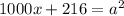 ; Взяв это равенство по модулю 3, получим:
; Взяв это равенство по модулю 3, получим: 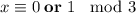 (так как квадрат числа дает остаток или 1, или 0 при делении на 3).
(так как квадрат числа дает остаток или 1, или 0 при делении на 3).
Значит, x равен 1, 3, 4, 6, 7 или 9. (можно было объяснить проще: x+2+1+6 - сумма цифр искомого числа дает тот же остаток от деления на 3, что и само число [известное свойство], откуда и вытекает полученное). Можно перебрать оставшиеся числа, а можно предположить, что число делится на три. Тогда остаются числа 3, 6, 9. Более того, искомое число делится и на 4. Значит, число делится на 12. Осталось проверить квадраты чисел 36, 48, 60, 72, 84, 96. Но искомое число оканчивается на 6, поэтому к рассмотрению подлежат лишь 36 и 96. Легкой проверкой убеждаемся, что 96 подходит. Искомое число - 9216