Пусть сторона квадрата равна а cм, тогда периметр квадрата можно найти по формуле: Р = 4 ∙ а, площадь квадрата по формуле: S = а².
1). Если а = 256 мм, то Р = 4 ∙ 256 = 1024 (мм); если а = 300 см, то Р = 4 ∙ 300 = 1200 (см); если а = 4 м 30 см = 430 см, то Р = 4 ∙ 430 = 1720 (см).
2). Если а = 500 см, то S = 500² = 250000 (см²); если а = 60 см, то S = 60² = 3600 (см²); если а = 70 дм, то S = 70² = 4900 (дм²).
3). Если P = 420 мм, то а = Р : 4; а = 420 : 4 = 105 (мм); если P = 12 дм 4 см = 124 см, то а = 124 : 4 = 31 (см); если P = 5 м 80 см = 580 см, то а = 580 : 4 = 145 (см).
4). Если S = 1600 см², то подбором находим сторону а = 40 см; если S = 8100 дм², то подбором находим сторону а = 90 дм; если S = 490 000 мм², то подбором находим сторону а = 700 мм.
АВ- диаметр окружности. Тогда О- середина отрезка АВ является центром окружности.
O( 1; 3) - центр окружности.
R= AO
Тогда уравнение окружности принимает вид:
2) Окружность имеет центр в точке (1; -2). Тогда уравнение окружности принимает вид:
Найдем радиус окружности, зная, что окружность проходит через точку (3;-4)
Значит, уравнение окружности
3) Центр окружности начало координат, то есть точка О(0;0),
4) Точки А(-4;1), В( 4;9), С( 14;1) лежат на окружности, значит, координаты этих точек удовлетворяют уравнению окружности. Поэтому подставим координаты данных точек в общее уравнение и решим систему уравнений.
Решим последнее уравнение системы.
Подставим найденное значение во второе уравнение системы
Пусть сторона квадрата равна а cм, тогда периметр квадрата можно найти по формуле: Р = 4 ∙ а, площадь квадрата по формуле: S = а².
1). Если а = 256 мм, то Р = 4 ∙ 256 = 1024 (мм); если а = 300 см, то Р = 4 ∙ 300 = 1200 (см); если а = 4 м 30 см = 430 см, то Р = 4 ∙ 430 = 1720 (см).
2). Если а = 500 см, то S = 500² = 250000 (см²); если а = 60 см, то S = 60² = 3600 (см²); если а = 70 дм, то S = 70² = 4900 (дм²).
3). Если P = 420 мм, то а = Р : 4; а = 420 : 4 = 105 (мм); если P = 12 дм 4 см = 124 см, то а = 124 : 4 = 31 (см); если P = 5 м 80 см = 580 см, то а = 580 : 4 = 145 (см).
4). Если S = 1600 см², то подбором находим сторону а = 40 см; если S = 8100 дм², то подбором находим сторону а = 90 дм; если S = 490 000 мм², то подбором находим сторону а = 700 мм.
Пошаговое объяснение:
Уравнение окружности в общем виде
R- радиус окружности .
1) А( -2;8), В( 4; -2)
АВ- диаметр окружности. Тогда О- середина отрезка АВ является центром окружности.
O( 1; 3) - центр окружности.
R= AO
Тогда уравнение окружности принимает вид:
2) Окружность имеет центр в точке (1; -2). Тогда уравнение окружности принимает вид:
Найдем радиус окружности, зная, что окружность проходит через точку (3;-4)
Значит, уравнение окружности
3) Центр окружности начало координат, то есть точка О(0;0),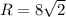
4) Точки А(-4;1), В( 4;9), С( 14;1) лежат на окружности, значит, координаты этих точек удовлетворяют уравнению окружности. Поэтому подставим координаты данных точек в общее уравнение и решим систему уравнений.
Подставим найденное значение во второе уравнение системы
Найдем радиус окружности
Тогда уравнение окружности принимает вид: