С какой скоростью ехал второй поезд, через 4 часа после выезда расстояние между ними стало равно 525 км.
U2 - ?
U1 = 13 км/час > S2
t = 4 часа
S = 525 км, но так как расстояние было ещё 41 км, то мы должны от 525 отнять 41 и получим 484 км. Тоесть 484 км они проехали без расстояние от станции.
Решение
Теперь найдём общую скорость с формулы:
S = U*t >> U = = = 121 км/час - общая скорость, но т.к. сказано что первый поезд двигался на 13 км/час быстрее чем второй. Значит:
U1 = + 6,5 = 67 - скорость первого поезда, а скорость второго будет:
U2 = - 6,5 = 54 - скорость второго поезда.
Теперь проверим: (67+54) * 4 = 484 км - теперь прибавим 41 км и получим 525 км, то есть условие выполнено, скорость второго поезда на 13 км меньше чем скорость первого, получилось выполнить условие задачи.
Скорость первого поезда на 13 км больше второго поезда.
Время движения 4 ч.
Расстояние между поездами 525 км.
Определить скорость второго поезда.
Перед решением, давай очень внимательно разберемся с условием задачи.
Из двух станций, расстояние между которыми 41 км, одновременно в противоположных направлениях выехали 2 поезда. Скорость первого поезда на 13 км/ч больше скорости второго поезда. Время движения поездов 4 ч, и расстояние между ними после выезда стало 525 км. Поезда двигались в разных направлениях, значит за 4 часа каждый поезд, двигаясь со своей скоростью, проехал свое расстояние. Согласно условию задачи, в начале движения между поездами расстояние уже было 41 км, значит фактически оба поезда проехали 525 – 41 = 484 км.
Примем скорость второго поезда (v1) за х км/ч. Тогда скорость первого поезда (v2) равна (х +13) км/ч.
Расстояние, на которое удаляются поезда за единицу времени, называют скоростью удаления vуд.
В этом случае скорость удаления vуд = v1 + v2, км/ч
Через t часов между поездами будет расстояние:
Sуд = vуд * t = (v1 + v2) * t, км
Составим уравнение:
(х + (х + 13)) * 4 = 484
(х + х + 13) * 4 = 484
(2х + 13) * 4 = 484
8х + 52 = 484
8х = 484 – 52
8х = 432
х = 432 : 8
х = 54
Скорость второго поезда равно 54 км/ч.
Скорость первого поезда равно: 54 + 13 = 67 км/ч.
ответ: скорость второго поезда 54 км/ч.
Проверка:
Определим расстояние, которое проехал каждый поезд по формуле:
S = v * t, где s — пройденный путь (км), v — скорость движения (км/ч), t — время (ч), за которое пройден путь S.
Расстояние, которое проехал первый поезд:
S1 = 67 * 4 = 268 км.
Расстояние, которое проехал второй поезд:
S2 = 54 * 4 = 216 км.
Сумма расстояний, которые проехал первый поезд и расстояние, которое проехал второй поезд, фактически проехали два поезда.
S3 = S1 - S2, км
S3 = 268 + 216 = 484 км.
В начале движения между поездами расстояние уже было 41 км, значит расстояние между поездами составит: 484 + 41 = 525 км.
Скорость второго поезда 54 км/час
Пошаговое объяснение:
Общее расстояние станций - 41 км
Поезд с А проезжает на 13км больше чем поезд Б
С какой скоростью ехал второй поезд, через 4 часа после выезда расстояние между ними стало равно 525 км.
U2 - ?
U1 = 13 км/час > S2
t = 4 часа
S = 525 км, но так как расстояние было ещё 41 км, то мы должны от 525 отнять 41 и получим 484 км. Тоесть 484 км они проехали без расстояние от станции.
Решение
Теперь найдём общую скорость с формулы:
S = U*t >> U =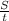
= 
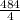= 121 км/час - общая скорость, но т.к. сказано что первый поезд двигался на 13 км/час быстрее чем второй. Значит:
U1 =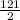
+ 6,5 = 67 - скорость первого поезда, а скорость второго будет:
U2 =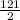
- 6,5 = 54 - скорость второго поезда.
Теперь проверим: (67+54) * 4 = 484 км - теперь прибавим 41 км и получим 525 км, то есть условие выполнено, скорость второго поезда на 13 км меньше чем скорость первого, получилось выполнить условие задачи.
Пошаговое объяснение:
Расстояние между станциями 41 км.
Направление движения: противоположное.
Выехали из двух станций одновременно.
Скорость первого поезда на 13 км больше второго поезда.
Время движения 4 ч.
Расстояние между поездами 525 км.
Определить скорость второго поезда.
Перед решением, давай очень внимательно разберемся с условием задачи.
Из двух станций, расстояние между которыми 41 км, одновременно в противоположных направлениях выехали 2 поезда. Скорость первого поезда на 13 км/ч больше скорости второго поезда. Время движения поездов 4 ч, и расстояние между ними после выезда стало 525 км. Поезда двигались в разных направлениях, значит за 4 часа каждый поезд, двигаясь со своей скоростью, проехал свое расстояние. Согласно условию задачи, в начале движения между поездами расстояние уже было 41 км, значит фактически оба поезда проехали 525 – 41 = 484 км.
Примем скорость второго поезда (v1) за х км/ч. Тогда скорость первого поезда (v2) равна (х +13) км/ч.
Расстояние, на которое удаляются поезда за единицу времени, называют скоростью удаления vуд.
В этом случае скорость удаления vуд = v1 + v2, км/ч
Через t часов между поездами будет расстояние:
Sуд = vуд * t = (v1 + v2) * t, км
Составим уравнение:
(х + (х + 13)) * 4 = 484
(х + х + 13) * 4 = 484
(2х + 13) * 4 = 484
8х + 52 = 484
8х = 484 – 52
8х = 432
х = 432 : 8
х = 54
Скорость второго поезда равно 54 км/ч.
Скорость первого поезда равно: 54 + 13 = 67 км/ч.
ответ: скорость второго поезда 54 км/ч.
Проверка:
Определим расстояние, которое проехал каждый поезд по формуле:
S = v * t, где s — пройденный путь (км), v — скорость движения (км/ч), t — время (ч), за которое пройден путь S.
Расстояние, которое проехал первый поезд:
S1 = 67 * 4 = 268 км.
Расстояние, которое проехал второй поезд:
S2 = 54 * 4 = 216 км.
Сумма расстояний, которые проехал первый поезд и расстояние, которое проехал второй поезд, фактически проехали два поезда.
S3 = S1 - S2, км
S3 = 268 + 216 = 484 км.
В начале движения между поездами расстояние уже было 41 км, значит расстояние между поездами составит: 484 + 41 = 525 км.
Задача решена верно.