Для того что бы упростить данное тригонометрическое выражение нам понадобится знание основных тригонометрических формул. В этом выражении мы будем использовать вот эти формулы:
Cos^2x + sin^2x = 1;
1 + ctg^2x = 1 / ( sin^2x );
2. Подставим Cos^2x + sin^2x = 1, в наше выражение и получим:
Cos^2x + sin^2x + ctg^2x = 1 + ctg^2x =
3. Далее подставим формулу 1 + ctg^2x = 1 / ( sin^2x ), и получим:
Пошаговое объяснение:
4) члены геометрической прогрессии
b₁=3к-2
b₂=2к
b₃=к+3
а)
мы знаем, что отношение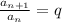 , составим такие отношения
, составим такие отношения
b) теперь строим прогрессии
для k₁ = 1 : b₁=3*1-2=1; b₂=2*1=2; b₃=1+3= 4 это возрастающая прогресстя
для k₂ = 6 b₁=3*6-2=16; b₂=2*6=12; b₃=6+3= 9 - это бесконечно убывающая геометрическая прогрессия, ее сумма
5.
рассуждаем так, в каждом последующем ряду бревен будет на 1 меньше, тогда n-член арифметической прогрессии имеет вид
12-(n-1)=1 ⇒ n=12
найдем сумму 12 членов арифметической прогрессии
Cos^2x + sin^2x + ctg^2x = 1 / ( sin^2x ).
Пошаговое объяснение:
Для того что бы упростить данное тригонометрическое выражение нам понадобится знание основных тригонометрических формул. В этом выражении мы будем использовать вот эти формулы:
Cos^2x + sin^2x = 1;
1 + ctg^2x = 1 / ( sin^2x );
2. Подставим Cos^2x + sin^2x = 1, в наше выражение и получим:
Cos^2x + sin^2x + ctg^2x = 1 + ctg^2x =
3. Далее подставим формулу 1 + ctg^2x = 1 / ( sin^2x ), и получим:
=1 + ctg^2x = 1 / ( sin^2x );
ответ: Cos^2x + sin^2x + ctg^2x = 1 / ( sin^2x ).