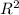". Я искала по интернету, но мне кажется это еще не всё. Формулы: каноническое уравнение прямой на плоскости; уравнение прямой, проходящей через 2 точки, уравнение пучка прямых; параметрические уравнения; общие уравнения прямой; уравнения прямой, проходящей через точку; уравнение для нахождения проекции точки на прямую, заданную уравнением l: Ax+By+C=0. Еще буду очень благодарна, если приведете какие-нибудь примеры задач по этой теме: нахождение проекции точки на прямую, нахождение уравнение прямой L1 через нахождение прямой уравнения L параллельно и перпендикулярно прямой L и так далее. Чем больше примеров, тем лучше. Кто сделает наиболее понятно, то поставлю "лучший ответ"
1. Мы знаем, что 4 игры были сыграны вничью а всего было 28 игр, поэтому сразу производим следующее действие: 28-4=24 игры команда выиграла или проиграла
2. Дальше, мы знаем, что выигрышей в 3 раза больше чем поражений, значит 3/4 из 24 игр это победы и 1/4 это поражения.
3. Теперь мы должны узнать чему равняется 1/4, для этого 24:4=6, таким образом получается, что команда проиграла 6 игр (ведь поражений было 1/4 от 24 игр, а мы узнали, что 1/4=6)
4. А теперь узнаем сколько игр команда выиграла: 24-6=18 игр команда выиграла
Сравнение дробей с одинаковыми знаменателями по сути является сравнением количества одинаковых долей. К примеру, обыкновенная дробь 3/7 определяет 3доли 1/7, а дробь 8/7 соответствует 8 долям 1/7, поэтому сравнение дробей с одинаковыми знаменателями 3/7 и 8/7 сводится к сравнению чисел 3 и 8, то есть, к сравнению числителей.
Из этих соображений вытекает правило сравнения дробей с одинаковыми знаменателями: из двух дробей с одинаковыми знаменателями больше та дробь, числитель которой больше, и меньше та дробь, числитель которой меньше.
Озвученное правило объясняет, как сравнить дроби с одинаковыми знаменателями. Рассмотрим пример применения правила сравнения дробей с одинаковыми знаменателями.
Пример.
Какая дробь больше: 65/126 или 87/126?
Решение.
Знаменатели сравниваемых обыкновенных дробей равны, а числитель 87дроби 87/126 больше числителя 65 дроби 65/126 (при необходимости смотрите сравнение натуральных чисел). Поэтому, согласно правилу сравнения дробей с одинаковыми знаменателями, дробь 87/126 больше дроби 65/126.
.