Искомое двузначное число представим в виде ( и - однозначные и неотрицательные, при этом ).
1). Пусть зачеркнули цифру из разряда десятков. Тогда из числа получилось число . Нам нужно выполнение следующего равенства:
Единственные однозначные натуральные решения: и .
Значит, число ⇒ .
2). Пусть зачеркнули цифру из разряда единиц. ⇒ . Уравнение составляется и решается по аналогии:
Откуда и .
Имеем второе подходящее решение: ⇒ .
Значит, двузначное число - это или , или .
Решение 2:
Можно было и кратким подбором решить, умножая все цифры на (умножаемая цифра - та, которая могла остаться после вычеркивания), пока не станут появляться трехзначные числа.
Нам нужно, чтобы в получившемся числе присутствовало умножаемое число (иначе как оно смогло бы потом остаться?):
1. раскрыть скобки. для этого умножим член, стоящий за скобкой на каждый член в скобке.
2. раскидываем получившиеся многочлены на две стороны: выражения с переменными идут в левую часть, без переменных- в правую. если так получилось, что выражение с переменной находится справа от знака =, то переносишь это выражение налево, но изменив знак. например, если справа от = получилось -3х, то переносишь это влево, но уже пишешь 3х. если было 3х, то пишем -3х. также и с выражениями, не имеющих переменных.
3.приводим подобные: выражения только с одинаковой буквой складываем, вычитаем. выражения только без переменных складываем\вычитаем.
4.освобождаем х- если рядом с ним стояла цифра, то переносим ее вправо без х со знаком деления.
1) зачеркнули 7 из числа 17;
2) зачеркнули 8 из числа 85.
Решение 1:Искомое двузначное число представим в виде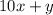
(
и 
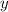- однозначные и неотрицательные, при этом 
).
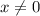1). Пусть зачеркнули цифру из разряда десятков. Тогда из числа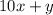
получилось число 
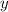. Нам нужно выполнение следующего равенства:
Единственные однозначные натуральные решения: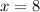
и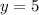 
.
Значит, число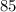
⇒ 
.
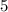2). Пусть зачеркнули цифру из разряда единиц.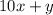
⇒ 
. Уравнение составляется и решается по аналогии:
Откуда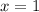
и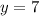 
.
Имеем второе подходящее решение: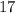
⇒ 
.
Значит, двузначное число - это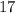 или
, или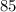 
.
Решение 2:Можно было и кратким подбором решить, умножая все цифры на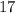
(умножаемая цифра - та, которая могла остаться после вычеркивания), пока не станут появляться трехзначные числа.
Нам нужно, чтобы в получившемся числе присутствовало умножаемое число (иначе как оно смогло бы потом остаться?):
Получаем те же самые два решения: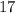
и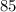 
.
Задача решена!объясню для тебя как решать такие уравнения)
здесь такой алгоритм:
1. раскрыть скобки. для этого умножим член, стоящий за скобкой на каждый член в скобке.
2. раскидываем получившиеся многочлены на две стороны: выражения с переменными идут в левую часть, без переменных- в правую. если так получилось, что выражение с переменной находится справа от знака =, то переносишь это выражение налево, но изменив знак. например, если справа от = получилось -3х, то переносишь это влево, но уже пишешь 3х. если было 3х, то пишем -3х. также и с выражениями, не имеющих переменных.
3.приводим подобные: выражения только с одинаковой буквой складываем, вычитаем. выражения только без переменных складываем\вычитаем.
4.освобождаем х- если рядом с ним стояла цифра, то переносим ее вправо без х со знаком деления.
5. считаем выражение справа и получаем х!
посмотрим на твоих примерах:
1) 1. 4(а+10)+5(3а+3)=93
4а+40+15а+15=93
2. 15а+4а=93-55
3. 19а=38
4. а=38\19
а=2
ответ: 2
2) 1. 30х-50=10х+10
2. 30х-10х=10+50
3. 20х=60
4. х= 60\20
х=3
ответ:3
3) 1. 35-9у-27-2=25-10у
2. -9у+10у=25-35+27+2
3. у=19
ответ: 19