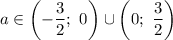Обозначим Как известно, площадь параллелограмма равна длине вектора, который называется векторным произведением векторов с и d Выразим веторное произведение векторов с и d через данные векторы a и b × - знак векторного произведения.
Использованы дистрибутивные законы, скобки раскрыты по правилу умножения многочленов. Во втором слагаемом используем свойство антикоммутативности векторного произведения.
Векторное произведение вектора а на вектор b численно равно площади параллелограмма построенного на векторах а и b:
S параллелограмма построенного на векторах c и d в три раза больше ответ. 12 кв ед
Как известно, площадь параллелограмма равна длине вектора, который называется векторным произведением векторов с и d
Выразим веторное произведение векторов с и d через данные векторы a и b
× - знак векторного произведения.
Использованы дистрибутивные законы, скобки раскрыты по правилу умножения многочленов. Во втором слагаемом используем свойство антикоммутативности векторного произведения.
Векторное произведение вектора а на вектор b численно равно площади параллелограмма построенного на векторах а и b:
S параллелограмма построенного на векторах c и d в три раза больше
ответ. 12 кв ед
Первый аналитический)
1) Если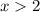 , то
, то 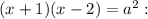
Проверим условие
Таким образом, если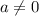 , то имеем корень
, то имеем корень 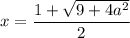
2) Если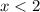 , то
, то 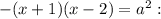
Найдем такие значения , при которых
, при которых 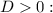
Тогда корни:
Проверим условие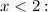
С учетом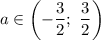 имеем:
имеем: 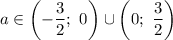
Таким образом, при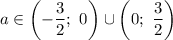 имеем три корня.
имеем три корня.
Второй графический)
Рассмотрим две функции:
Изобразим на координатной плоскости функцию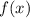
1) Если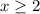 , то
, то 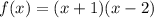 — квадратичная функция, график — парабола, ветви параболы направлены вверх
— квадратичная функция, график — парабола, ветви параболы направлены вверх
2) Если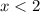 , то
, то 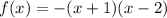 — квадратичная функция, график — парабола, ветви параболы направлены вниз
— квадратичная функция, график — парабола, ветви параболы направлены вниз
Вершина параболы: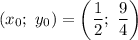
Изобразим данные функции на соответствующих участках (см. вложение).
Уравнение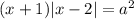 будет иметь три корня, если будет три пересечения графика функции
будет иметь три корня, если будет три пересечения графика функции  c
c 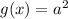
Так будет, если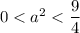 или
или 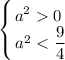
Решением системы будет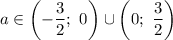
Таким образом, при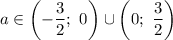 имеем три корня.
имеем три корня.
ответ: