Математика: , нужно решить по формуле гауса и крауса

, нужно решить по формуле гауса и крауса

Показать ответ

Ответ:

hyrshkananastasiya

07.02.2021 23:08

1-ая задача: 1 минута - 1 литр

2-ое задание: ответ в объяснении

3-е задание: в картинке

4-ое задание: 1-ое = 316; 2-ое = 15

5-ое задание: ответ в объяснении

6-ое задание: ответ в объяснении

7-ая задача: 10 кочанов капусты на 20 ложек соли

Пошаговое объяснение:

1-ая задача:

Дано:

3 минуты - 3 литра воды

1 минута - ?

1) 3 минуты ÷ 3 литра воды = 3 ÷ 3 = 1 (литр) - на одну минуту уходит

2) 1 минута = 1 литру

ответ: 1 минута - 1 литр

2-ое задание:

72 ÷ (82-78) × 2 = 72 ÷ 4×2 = 36 (первым действием - скобки)

19 + 17 × 4 - 38 = 19 + 68 - 38 = 49 (первым действием - умножение)

5 × (3 × 28 - 73) = 5 × (84 - 73) = 5 × 11 = 55 (первым действием - в скобках, умножение)

7 × (4 × 19 - 65) = 7 × (76 - 65) = 7 × 11 = 77 (первым действием - в скобках, умножение)

3-е задание:

В картинке

4-ое задание:

1) 700 - х = 384

- х = 384 - 700

- х = - 316

х = 316 (минуса сокращаем)

2) 90 ÷ у = 6

у = 90 ÷ 6

у = 15

5-ое задание:

4м 5см (4,05м) < 450см (4,5м)

8дм 2см (82 см) < 8м 2см (802см)

2мин 15с (135с) > 115с

3ч 12мин (192мин) > 182мин

6-ое задание:

Дано:

a = 1дм = 10см

b = a ÷ 2

Найти:

P - ?

S - ?

1) b = a ÷ 2 = 10см ÷ 2 = 5 (см)

2) P = 2 × (a + b) = 2 × (10 + 5) = 30 (см) - периметр

3) S = a × b = 10 × 5 = 50 (см^{2}) - площадь

ответ: P = 30см; S = 50 см^{2}

7-ая задача:

Дано:

2 кочана капусты = 4 ложки соли

Х кочанов капусты = 20 ложек соли

Найти:

X - ?

1) 4 ложки соли ÷ 2 кочана капусты = 2 ложки соли - уходит на 1 кочан капусты

2) 20 ложек соли ÷ 2 ложки соли = 10 кочанов капусты

ответ: 10 кочанов капусты на 20 ложек соли

с этими заданиями.Задачи1 и7 составить краткую запись на задачи кто может

0,0(0 оценок)

Ответ:

hashedhashed1

23.11.2020 06:03

$\dfrac{7}{66}$

Пошаговое объяснение:

Воспользуемся формулой числа сочетаний:

$C^m_n=\dfrac{n!}{(n-m)!\times m!}$

Тогда всего сочетаний:

$C^5_{11}=\dfrac{11!}{(11-5)!\times5!}=330$

Сочетаний, где хотя бы 4 книги - детективы:

$C^4_7=\dfrac{7!}{(7-4)!\times4!}=35$

Тогда ответом будет:

$P=\dfrac{35}{330}=\dfrac{7}{66}\approx0.1$

Задачу можно решить, не зная формулы выше, следующим

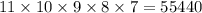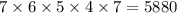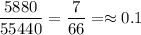Всего существует $11\times10\times9\times8\times7=55440$ комбинаций выбора 5-ти книг из 11 (здесь учитывается расположение каждой книги, поэтому числа получаются больше). $7\times6\times5\times4\times7=5880$ , случаев, которые подходят по условию. Откуда получили вероятность $\dfrac{5880}{55440}=\dfrac{7}{66}=\approx0.1$ .