На доске написано натуральное четырехзначное число. Известно, что при делении этого числа на сумму его цифр получалось число 71. Определите это число.
ответ: было записано число 1278.
Задача №2:
На доске написано три трехзначных натуральных числа. Известно, что сумма цифр каждого не превышает 9. Была найдена сумма цифр каждого числа (под каждым исходным числом на доске записали соответствующее однозначное число). Найденные числа расположили друг за другом в порядке возрастания без промежутков так, что получилось новое трехзначное число. Возможно ли, что при делении суммы трех исходных трехзначных чисел на полученное трехзначное число получится целое число X, причем наибольшее из трех исходных чисел должно делиться на наименьшее из них без остатка так, чтобы в результате такого деления получалось число X-1.
ответ: да, возможно, например, это числа 100, 210, 500.
Задача №3:
Было загадано три различных натуральных двузначных числа: a, b и c. Может ли следующее равенство быть верным: .
(см. объяснение)
Пошаговое объяснение:
В своем ответе приведу три составленные задачи:
Задача №1:
На доске написано натуральное четырехзначное число. Известно, что при делении этого числа на сумму его цифр получалось число 71. Определите это число.
ответ: было записано число 1278.
Задача №2:
На доске написано три трехзначных натуральных числа. Известно, что сумма цифр каждого не превышает 9. Была найдена сумма цифр каждого числа (под каждым исходным числом на доске записали соответствующее однозначное число). Найденные числа расположили друг за другом в порядке возрастания без промежутков так, что получилось новое трехзначное число. Возможно ли, что при делении суммы трех исходных трехзначных чисел на полученное трехзначное число получится целое число X, причем наибольшее из трех исходных чисел должно делиться на наименьшее из них без остатка так, чтобы в результате такого деления получалось число X-1.
ответ: да, возможно, например, это числа 100, 210, 500.
Задача №3:
Было загадано три различных натуральных двузначных числа: a, b и c. Может ли следующее равенство быть верным: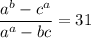 .
.
ответ: да, например, при a=31, b=32, c=10.
Задание выполнено!
ответ:85.6%
Пошаговое объяснение:
Дождь идет всего час, поэтому рассмотрим 3 случая.
1 - Дождь пошел в 13 часов, но не шел в 14 и 15, вероятность этого 0.6*0.6*0.6=0.216
2 - Дождь пошел в 14, но не шел в 13 и 15 часов, вероятность - 0.4*0.4*0.6=0.096
3 - Дождь пошел в 15, но не шел в 13 и 14, вероятность - 0.4*0.6*0.4=0.096
Эти события несовместные, поэтому складываем вероятности и получаем 0.408
В процентах это будет 40.8% (можно округлить до 41, но это уже на вас)
Забудь про эту часть, я сначала не допер до того, что это события зависимые, поэтому решать надо по-другому.
Допустим, что дождь не пойдет вообще, вероятность этого 0.4*0.6*0.6=0.144
Тогда вероятность того, что дождь пойдет хотя бы раз будет равна 1-0.144=0.856
В процентах 85.6 (округление до 86)