Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
vavavvavavavava
03.05.2021 20:43 •
Математика
Обчислить границу стремящуюся к нулю
Показать ответ
Ответ:
Викуля20172006
10.10.2020 16:32
в) +∞
Пошаговое объяснение:
в) Используем тригонометрические тождества
1)
2)
0,0
(0 оценок)
Популярные вопросы: Математика
tesaf
29.08.2020 16:01
Прочитай в одной коробке 9 карандашей.сколько останется в пяти таких же коробках,если из каждой взять по 2карандаша? запиши решение двумя...
tdtwdgtduqgcggggc
29.08.2020 16:01
Площадь карагандинской области 428 000 км в квадрате ,костанайской области - 196 000 км в квадрате , восточно - казахстанский области - 283 300 км в квадрате ....
Назмина134
29.08.2020 16:01
Используя цифры 1, 7, 3, 8, 6, запиши место х десятичную дробить, чтобы получилось верное двойное неравенство 1,3768 x 137, 68....
damila3434
29.08.2020 16:01
Подберите пропущеные числа []: 9=1(ост.6) []: 9=0(0ст.8)...
lanchik03
29.08.2020 16:01
Выращивание кристаллов соли, ответе на вопросы! сколько дней вы выращивали кристалл? какова его форма? какого цвета кристалл? прозрачный он или нет? каковы размеры...
sanek2031
29.08.2020 16:01
Как решить неравенство y-34 86 4класс...
Polklop
29.08.2020 16:01
Площать прямоугольника листа бумаги 16 дм2 а его длина 8 дм во сколько раз длина этого прямоугольника больше ширины...
полина10092003
29.08.2020 16:01
Найди градусную меру угла, если: a) 8/15 его равны72º; б) 2/3 его равны 60°; в) 7/4 его равны 280º....
13Sasharubakova
29.08.2020 16:01
Составьте таблицу четырех пар значений х и у х, у- целые числа, являющихся решениями уравнения 5x+2y=6...
gwetyalina1345
29.08.2020 16:01
Решить пример с целыми числами: 14-23-37+23+56-13...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
в) +∞
Пошаговое объяснение:
в) Используем тригонометрические тождества
1)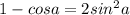
2)