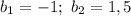Посчитаем, сколько всего существует четырехзначных чисел.
Минимальное из них 1000, максимальное 9999.
9999 - 999 = 9000 чисел.
Найдем количество чисел, у которых в записи все цифры четные.
На первой позиции у них стоит цифра 2, 4, 6, 8 - 4 варианта выбора.
На второй, третьей и четвертой позициях - любая из 5 цифр: 0, 2, 4, 6, 8 - по 5 вариантов.
Всего комбинаций 4 * 5 * 5 * 5 = 20 * 25 = 500.
9000 - 500 = 8500 чисел.
ответ: Существует 8500 четырехзначных чисел, у которых хотя бы одна цифра в записи нечетная.
Пошаговое объяснение:
График прямой задается формулой , где и — некоторые коэффициенты, — независимая переменная, которая называется линейной функцией.
Имеем три точки: , где — параметр, который нужно найти.
Подставляя соответствующие координаты в функцию, получаем систему из трех линейных уравнений с тремя неизвестными:
Из третьего уравнения: . Подставим в первое и во второе уравнение:
Выразим из второго уравнения :
Подставим в первое уравнение:
Решим полученное квадратное уравнение через дискриминант:
Таким образом, имеем:
ответ:
Посчитаем, сколько всего существует четырехзначных чисел.
Минимальное из них 1000, максимальное 9999.
9999 - 999 = 9000 чисел.
Найдем количество чисел, у которых в записи все цифры четные.
На первой позиции у них стоит цифра 2, 4, 6, 8 - 4 варианта выбора.
На второй, третьей и четвертой позициях - любая из 5 цифр: 0, 2, 4, 6, 8 - по 5 вариантов.
Всего комбинаций 4 * 5 * 5 * 5 = 20 * 25 = 500.
9000 - 500 = 8500 чисел.
ответ: Существует 8500 четырехзначных чисел, у которых хотя бы одна цифра в записи нечетная.
Пошаговое объяснение:
График прямой задается формулой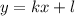 , где
, где 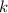 и
и 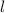 — некоторые коэффициенты,
— некоторые коэффициенты,  — независимая переменная, которая называется линейной функцией.
— независимая переменная, которая называется линейной функцией.
Имеем три точки: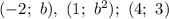 , где
, где 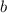 — параметр, который нужно найти.
— параметр, который нужно найти.
Подставляя соответствующие координаты в функцию, получаем систему из трех линейных уравнений с тремя неизвестными:
Из третьего уравнения: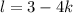 . Подставим
. Подставим 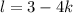 в первое и во второе уравнение:
в первое и во второе уравнение:
Выразим из второго уравнения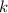 :
:
Подставим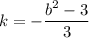 в первое уравнение:
в первое уравнение:
Решим полученное квадратное уравнение через дискриминант:
Таким образом, имеем: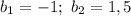
ответ: