Пример 1Метод: разложение интеграла суммы/разности на сумму/разность табличных интегралов.
Пример 2Метод: приведение под знак дифференциала.
Но так как степень n = 4 чётная, то отрицательного значения в аргументе логарифма быть не может, максимальное значение: ln|1 + 0| = ln|1| = 0, следовательно, модуль можно убрать.
Пример 3Метод: по частям.
Так как в подинтегральном выражении модуль, нужно рассматривать два случая:
Рассмотрим первый интеграл:
Второй интеграл отличается от первого знаком минус в аргументе, поэтому ответ будет таким же, различаться будут лишь аргументы (это исключительный случай)
Так как это кусочно-заданная функция
, нам необходимо написать условия для отдельных формул. Так, для I₁ условие x ≥ 0, а для I₂ < 0.
Обозначим макет того, что должно у нас выйти
В числе 52314 5 цифр, мы точно знаем, что последняя - это "1", тогда у нас остаётся 4 цифры, которые мы можем поставить как нам угодно
Вне зависимости от того, с какого порядка мы начнём (c X1 или X2, или X3 - неважно), количество вариантов останется неизменным
Начнём с X1
на X1 - могут быть поставлены 5, 2, 3, 4 т.е 4 возможных случая
на Х2 уже могут поставлены уже 3 цифры, так как в предыдущем случае мы уже выбрали одну, и осталось 3 свободных цифры. И так далее
на X3 - 2 цифры
на X4 - 1 цифра
Если бы начали в другом ином порядке, смысл задачи и ответ на неё от этого не поменяется
Значит число возможных пятизначных чисел =
P=4! = 4*3*2*1 = 24 возможных комбинаций
ответ: 24
Пример 2Метод: приведение под знак дифференциала.Но так как степень n = 4 чётная, то отрицательного значения в аргументе логарифма быть не может, максимальное значение: ln|1 + 0| = ln|1| = 0, следовательно, модуль можно убрать.
Пример 3Метод: по частям.Так как в подинтегральном выражении модуль, нужно рассматривать два случая:
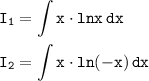
Рассмотрим первый интеграл: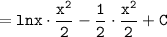
Второй интеграл отличается от первого знаком минус в аргументе, поэтому ответ будет таким же, различаться будут лишь аргументы (это исключительный случай)Так как это кусочно-заданная функция
, нам необходимо написать условия для отдельных формул. Так, для I₁ условие x ≥ 0, а для I₂ < 0.