За кулисами цирка толпятся артисты, народ веселый и беспечный. Среди них выделяется уже не слишком молодой лысый человек, чье лицо густо раскрашено белым и красным. Это клоун Эдварде, вступивший в "период тоски", за которым последует период тяжкою запоя. Эдварде - главное украшение цирка, его приманка, но поведение клоуна ненадежно, в любой день он может сорваться и запить.Режиссер просит Эдвардса продержаться хотя бы еще два дня, до конца масленицы, а там уже и цирк закроется на время поста. Клоун отделывается ничего не значащими словами и заглядывает в уборную акробата Беккера, грубого мускулистого великана.Интересует Эдвардса не Беккер, а его питомец, "гуттаперчевый мальчик", подручный акробата. Клоун просит разрешения погулять с ним, доказывая Беккеру, что после отдыха и развлечения маленький артист станет лучше работать. История "гуттаперчевого мальчика" была проста и печальна. После смерти матери её землячка, прачка Варвара, устроила судьбу сироты, определив его в ученье к Беккеру. При первой встрече с Петей Карл Богданович грубо и больно ощупал раздетого догола мальчика, замершего от боли и ужаса. Как он ни плакал, как ни цеплялся за подол прачки, Варвара отдала его в полное владение акробату. В один из последних дней масленицы графские дети были особенно оживлены. Ещё бы! Тетя Соня, сестра их матери, обещала повести их в пятницу в цирк. Наконец наступает долгожданная пятница. И вот уже все волнения и страхи позади. Дети усаживаются на свои места задолго до начала представления. Им все интересно. С неподдельным восторгом смотрят дети на наездницу, жонглера и клоунов, предвкушая встречу с гуттаперчевым мальчиком.
Пусть x овощей имеют массу меньше 1000, y - больше 1000, а z - ровно 1000.
а) Предположим, что да. Тогда справедливо уравнение:
, но x очевидно не может быть нулем, т.к. среднее арифметическое больше нуля. Противоречие.
б) Предположим, что это возможно. Тогда x+y+13=65 ⇔ x+y=52. Аналогично строим уравнение: , получили противоречие: x должно быть целым числом.
в) Понятно, что минимальная масса встречается только в группе, где расположены овощи массой меньше 1000 г. Обозначим массу самого легкого за ; Пусть масса оставшихся в этой же группе овощей суммарно равна ; Тогда ; Заметим, что ; Поэтому (*);
Теперь рассмотрим уравнение , значит x кратно 4. Пусть ;
Рассмотрим другое уравнение: ; Отсюда получаем, что ;
Возвратимся к (*): ; Приведем пример при котором осуществима оценка:
Пусть в первой группе 1 овощ весит 387 граммов, а остальные 35 весят по 999 граммов. Во второй группе 2 овоща весят по 1000 граммов. А в последней группе 27 овощей весят 1024 грамма.
В один из последних дней масленицы графские дети были особенно оживлены. Ещё бы! Тетя Соня, сестра их матери, обещала повести их в пятницу в цирк. Наконец наступает долгожданная пятница. И вот уже все волнения и страхи позади. Дети усаживаются на свои места задолго до начала представления. Им все интересно. С неподдельным восторгом смотрят дети на наездницу, жонглера и клоунов, предвкушая встречу с гуттаперчевым мальчиком.
Пусть x овощей имеют массу меньше 1000, y - больше 1000, а z - ровно 1000.
а) Предположим, что да. Тогда справедливо уравнение:
б) Предположим, что это возможно. Тогда x+y+13=65 ⇔ x+y=52. Аналогично строим уравнение: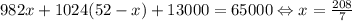
, получили противоречие: x должно быть целым числом.
в) Понятно, что минимальная масса встречается только в группе, где расположены овощи массой меньше 1000 г. Обозначим массу самого легкого за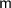
; Пусть масса оставшихся в этой же группе овощей суммарно равна 
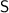; Тогда 
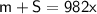; Заметим, что 
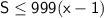; Поэтому 
(*);
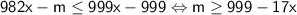Теперь рассмотрим уравнение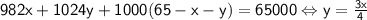
, значит x кратно 4. Пусть 
;
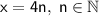Рассмотрим другое уравнение: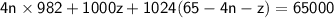
; Отсюда получаем, что 
;
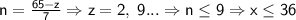Возвратимся к (*):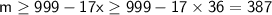
; Приведем пример при котором осуществима оценка:
Пусть в первой группе 1 овощ весит 387 граммов, а остальные 35 весят по 999 граммов. Во второй группе 2 овоща весят по 1000 граммов. А в последней группе 27 овощей весят 1024 грамма.
ответ: а) нет
б) нет
в) минимально возможная масса - 387 граммов