Если убрать две первые цифры, то получится двузначное число, которое, согласно условию, является четвертой степенью целого числа. Среди двузначных чисел таких всего два: 16=2⁴ и 81=3⁴;
Если убрать первую цифру слева, то получим трехзначное число - куб по условию. Кубов среди трехзначных чисел немного, вот они: 5³, 6³, 7³, 8³ и 9³. При этом последние две цифры должны быть 16 или 81 (см. выше).
Таким образом, подходит только 6³. Остается найти число x такое, что x216 - квадрат. Можно записать: ; Взяв это равенство по модулю 3, получим: (так как квадрат числа дает остаток или 1, или 0 при делении на 3).
Значит, x равен 1, 3, 4, 6, 7 или 9. (можно было объяснить проще: x+2+1+6 - сумма цифр искомого числа дает тот же остаток от деления на 3, что и само число [известное свойство], откуда и вытекает полученное). Можно перебрать оставшиеся числа, а можно предположить, что число делится на три. Тогда остаются числа 3, 6, 9. Более того, искомое число делится и на 4. Значит, число делится на 12. Осталось проверить квадраты чисел 36, 48, 60, 72, 84, 96. Но искомое число оканчивается на 6, поэтому к рассмотрению подлежат лишь 36 и 96. Легкой проверкой убеждаемся, что 96 подходит. Искомое число - 9216
Пошаговое объяснение:
7 1/3 ×9 = 1 + 7·3 /3 ×9 = 22 /3 ×9 = 22·9 /3 = 198 /3 = 66 · 3 /3 = 66 = 66
2 / 2 3 ×3 1 /4 = 2 + 2·3 /3 × 1 + 3·4/ 4 = 8 /3 × 13/ 4 = 8·13/ 3·4 = 104/ 12 = 26 · 4/ 3 · 4 = 26/ 3 = 8·3 + 2/ 3 = 8 2/ 3 ≈ 8.666666666666666
4 4 /7 ×3 5 /24 = 4 + 4·7/ 7 × 5 + 3·24 /24 = 32/ 7 × 77/ 24 = 32·77 /7·24 = 2464 168 = 44 · 56/ 3 · 56 = 44 /3 = 14·3 + 2/ 3 = 14 2 /3 ≈ 14.666666666666666
66 - 8 2/ 3 = 66 - 8 - 2/ 3 = 58 - 2/ 3 = 58·3 /3 - 2/ 3 = 174 3 - 2/ 3 = 174 - 2 /3 = 172/ 3 = 57·3 + 1/ 3 = 57 1/ 3 ≈ 57.333333333333336
57 1/ 3 - 14 2/3 = 1 + 57·3 /3 - 2 + 14·3 /3 = 172/ 3 - 44 /3 = 172 - 44 /3 = 128/ 3 = 42·3 + 2 /3 = 42 2 /3 ≈ 42.666666666666664
2)1 7/48× 2 2/5(9 1/6 4/15+2 5/9)×1/4=2 3/4-(2 4/9+2 5/9)×1/4=2 3/4-5× 1/4=2 3/4-1 1/4=1 1/2=1 1/2=1.5
Если убрать две первые цифры, то получится двузначное число, которое, согласно условию, является четвертой степенью целого числа. Среди двузначных чисел таких всего два: 16=2⁴ и 81=3⁴;
Если убрать первую цифру слева, то получим трехзначное число - куб по условию. Кубов среди трехзначных чисел немного, вот они: 5³, 6³, 7³, 8³ и 9³. При этом последние две цифры должны быть 16 или 81 (см. выше).
Таким образом, подходит только 6³. Остается найти число x такое, что x216 - квадрат. Можно записать: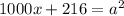
; Взяв это равенство по модулю 3, получим: 
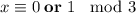(так как квадрат числа дает остаток или 1, или 0 при делении на 3).
Значит, x равен 1, 3, 4, 6, 7 или 9. (можно было объяснить проще: x+2+1+6 - сумма цифр искомого числа дает тот же остаток от деления на 3, что и само число [известное свойство], откуда и вытекает полученное). Можно перебрать оставшиеся числа, а можно предположить, что число делится на три. Тогда остаются числа 3, 6, 9. Более того, искомое число делится и на 4. Значит, число делится на 12. Осталось проверить квадраты чисел 36, 48, 60, 72, 84, 96. Но искомое число оканчивается на 6, поэтому к рассмотрению подлежат лишь 36 и 96. Легкой проверкой убеждаемся, что 96 подходит. Искомое число - 9216