Пошаговое объяснение:
Область определения любой функции не должна включать такие значения переменной, при который выражение не будет иметь смыста - перечислю основные
1) деление на 0
2) вычисления корня из отрицательного числа
3) логарифмирование отрицательного числа
Область значения - все значения, которые может принимать функция
Итак, приступим к выполнению задания
1) Посмотрим на функцию:
Никаких запрещённых операций нет. Так что
2) Посмотрим на функцию
Есть корень, значит подкоренное выражение (х + 1) должно быть больше или равно 0. Запишем или
Так как корень всегда положителен, то его значение всегда больше или равно 0.
3) Посмотрим на функцию
Видим корень, значит подкоренное выражение всегда больше или равно 0. Запишем
Так как корень всегда положителен, тогда
Тогда значения функции меньше или равны 2
4) Посмотрим на функцию:
Тут есть деление, значит мы не делим на 0, т.е. или
Тогда значения в точке 0 у функции не будет (числитель дроби 1)
5) Посмотрим на функцию
Здесь дробь. Тогда знаменатель не 0. То есть . Запишем
или
Дробь не может быть равна 0 так как числитель не 0.
Тогда
6) Посмотрим на функцию
Здесь есть дробь, значит сразу знаменатель не равен 0.
Преобразуем дробь.
Дробь определена при любых х, тогда
А) ответ в объяснении
Б) ответ в объяснении
С) ответ в объяснении
А) Признаки деления на 3:
Если все числа данного числа сложить и полученное делится на 3, то число делится на 3
2+9+5+6+6=28
Если вышло большое число, то ещё раз сложить
2+8=10, 10 на 3 не делится
Значит к этому числу нужно прибавить 2, чтобы вышло 12, а 12:3=4, и т.д.
ответ: 295662, 295665, 295668
Б) Признаки деления на 5:
Если число заканчивается на 5 или на 0, то оно делится на 5, тогда ответ: 295660, 295665
С) Признаки деления на 15:
Если число оканчивается на 0 или 5, а сумма цифр этого числа делится на 3, то и все число делится на 15.
2+8=10, 10 на 3 не делится, но делится на 5
Значит нужно прибавить 5, т.к. 15:3=5
Делится на 3,5, а значит и на 15
ответ: 295665
Можно лучший ответ?
Это 100% информация, у чела сверху неправильно
Пошаговое объяснение:
Область определения любой функции не должна включать такие значения переменной, при который выражение не будет иметь смыста - перечислю основные
1) деление на 0
2) вычисления корня из отрицательного числа
3) логарифмирование отрицательного числа
Область значения - все значения, которые может принимать функция
Итак, приступим к выполнению задания
1) Посмотрим на функцию: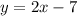
Никаких запрещённых операций нет. Так что
2) Посмотрим на функцию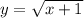
Есть корень, значит подкоренное выражение (х + 1) должно быть больше или равно 0. Запишем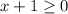 или
или 
Так как корень всегда положителен, то его значение всегда больше или равно 0.
3) Посмотрим на функцию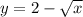
Видим корень, значит подкоренное выражение всегда больше или равно 0. Запишем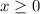
Так как корень всегда положителен, тогда
Тогда значения функции меньше или равны 2
4) Посмотрим на функцию: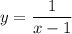
Тут есть деление, значит мы не делим на 0, т.е.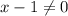 или
или 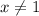
Тогда значения в точке 0 у функции не будет (числитель дроби 1)
5) Посмотрим на функцию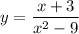
Здесь дробь. Тогда знаменатель не 0. То есть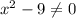 . Запишем
. Запишем
Дробь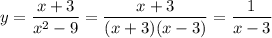 не может быть равна 0 так как числитель не 0.
не может быть равна 0 так как числитель не 0.
Тогда
6) Посмотрим на функцию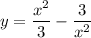
Здесь есть дробь, значит сразу знаменатель не равен 0.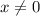
Преобразуем дробь.
Дробь определена при любых х, тогда
А) ответ в объяснении
Б) ответ в объяснении
С) ответ в объяснении
Пошаговое объяснение:
А) Признаки деления на 3:
Если все числа данного числа сложить и полученное делится на 3, то число делится на 3
2+9+5+6+6=28
Если вышло большое число, то ещё раз сложить
2+8=10, 10 на 3 не делится
Значит к этому числу нужно прибавить 2, чтобы вышло 12, а 12:3=4, и т.д.
ответ: 295662, 295665, 295668
Б) Признаки деления на 5:
Если число заканчивается на 5 или на 0, то оно делится на 5, тогда ответ: 295660, 295665
С) Признаки деления на 15:
Если число оканчивается на 0 или 5, а сумма цифр этого числа делится на 3, то и все число делится на 15.
2+9+5+6+6=28
2+8=10, 10 на 3 не делится, но делится на 5
Значит нужно прибавить 5, т.к. 15:3=5
Делится на 3,5, а значит и на 15
ответ: 295665
Можно лучший ответ?
Это 100% информация, у чела сверху неправильно